/Szkoła średnia/Funkcje/Z pierwiastkami/Zbiór wartości

Zadanie nr 4259840

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz najmniejszą i największą wartość funkcji 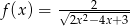----2----- f(x) = √2x2−4x+-3 na przedziale ⟨− 5,1 0⟩ .

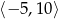Rozwiązanie

Ponieważ funkcja 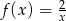2 f(x) = x jest malejąca dla 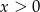x > 0 , wystarczy znaleźć punkty, w których wartości ekstremalne przyjmuje funkcja 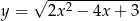√ ------------- y = 2x2 − 4x + 3 . Podobnie, ponieważ rosnąca jest funkcja 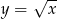y = √x-- , wystarczy zajmować się ekstremami funkcji 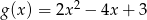2 g(x ) = 2x − 4x + 3 . No i jesteśmy w dobrze znanej sytuacji. Wykresem funkcji 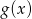g(x) jest parabola o ramionach skierowanych w górę, więc wartość najmniejszą przyjmuje w wierzchołku, czyli dla

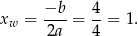
xw = −b-= 4-= 1. 2a 4

W tym punkcie będziemy mieli największą wartość wyjściowej funkcji (bo 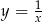y = 1x jest malejąca), równą

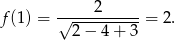
f(1) = √----2------= 2. 2− 4+ 3

Wartość największa funkcji 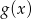g(x ) otrzymamy w jednym z końców przedziału. W którym? - liczymy.

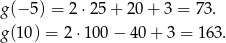
g (− 5) = 2⋅ 25+ 20+ 3 = 73. g (10) = 2 ⋅100 − 40 + 3 = 1 63.

Zatem najmniejszą wartość funkcji 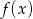f(x) otrzymamy dla 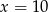x = 10 i jest ona równa

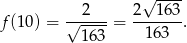
√ ---- f (10) = √-2--- = 2--1-63. 16 3 163

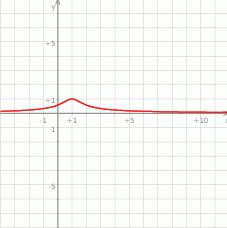
Na koniec, dla ciekawskich, wykres funkcji f(x) .

PIC

 
Odpowiedź: 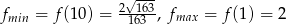√ --- fmin = f (10) = 2161633, fmax = f (1) = 2 .

Wersja PDF
Rozwiązanie Losuj ponownie