Zadanie nr 2007699
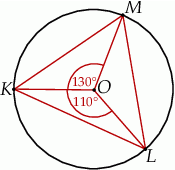
Punkt 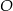 jest środkiem okręgu (zobacz rysunek). Miara kąta
jest środkiem okręgu (zobacz rysunek). Miara kąta 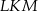 jest równa
jest równa
A) 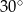 B)
B) 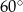 C)
C) 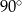 D)
D) 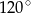
Rozwiązanie
Sposób I
Zauważmy, że każdy z trójkątów 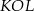 i
i 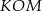 jest równoramienny. Mamy zatem
jest równoramienny. Mamy zatem
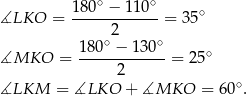
Sposób II
Korzystając z twierdzenia o kątach wpisanym i środkowym mamy
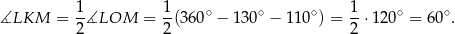
Odpowiedź: B

