Zadanie nr 2407478
Miara kąta wewnętrznego ośmiokąta foremnego jest równa:
A) 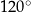 B)
B) 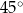 C)
C) 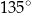 D)
D) 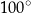
Rozwiązanie
Sposób I
Poprowadźmy przekątne ośmiokąta foremnego jak na lewym rysunku.
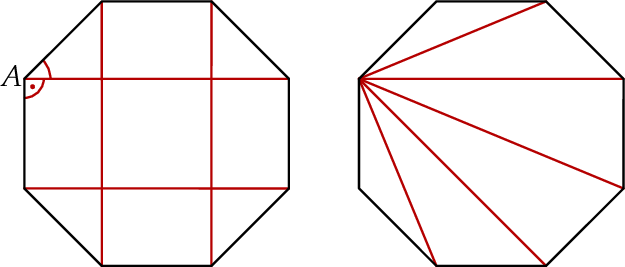
Widać teraz, że kąt przy wierzchołku ośmiokąta jest sumą kątów prostokąta i kąta ostrego w równoramiennym trójkącie prostokątnym. Ma on więc miarę
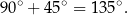
Sposób II
Prowadząc przekątne ośmiokąta wychodzące z jednego wierzchołka możemy podzielić ośmiokąt na 6 trójkątów (prawy rysunek). Zatem suma wszystkich kątów wewnętrznych ośmiokąta jest równa
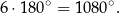
Jeden z kątów wewnętrznych ma więc miarę
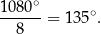
Sposób III
Korzystamy ze wzoru
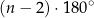
na sumę kątów wewnętrznych  –kąta. Suma kątów wewnętrznych ośmiokąta foremnego jest więc równa
–kąta. Suma kątów wewnętrznych ośmiokąta foremnego jest więc równa
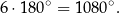
Jeden z kątów wewnętrznych ma zatem miarę
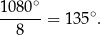
Odpowiedź: C

