Zadanie nr 9122612
Odcinek 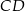 jest wysokością trójkąta
jest wysokością trójkąta 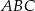 , w którym
, w którym 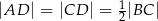 (zobacz rysunek). Okrąg o środku
(zobacz rysunek). Okrąg o środku 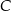 i promieniu
i promieniu 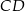 jest styczny do prostej
jest styczny do prostej 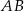 . Okrąg ten przecina boki
. Okrąg ten przecina boki 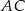 i
i 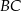 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 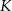 i
i 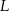 .
.
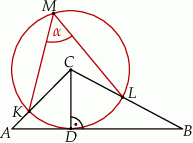
Zaznaczony na rysunku kąt  wpisany w okrąg jest równy
wpisany w okrąg jest równy
A) 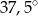 B)
B) 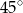 C)
C) 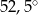 D)
D) 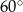
Rozwiązanie
Równość 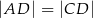 oznacza, że trójkąt
oznacza, że trójkąt 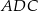 jest równoramiennym trójkątem prostokątnym, czyli
jest równoramiennym trójkątem prostokątnym, czyli 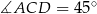 . Równość
. Równość 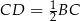 oznacza, że trójkąt
oznacza, że trójkąt 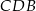 jest połówką trójkąta równobocznego, więc
jest połówką trójkąta równobocznego, więc 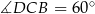 .
.
Teraz wystarczy skorzystać, z twierdzenia o kątach wpisanym i środkowym.
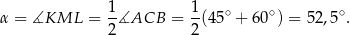
Odpowiedź: C

