Zadanie nr 9990604
Równanie 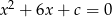 nie ma rozwiązania, gdy
nie ma rozwiązania, gdy
A) 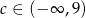 B)
B) 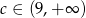 C)
C) 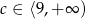 D)
D) 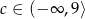
Rozwiązanie
Sposób I
Obliczamy wyznacznik równania
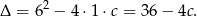
Funkcja kwadratowa nie posiada pierwiastków wtedy, gdy jej wyznacznik jest mniejszy od 0. Zatem
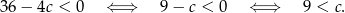
Sposób II
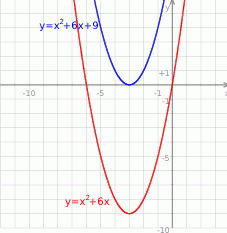
Wykresem funkcji 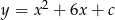 jest parabola
jest parabola 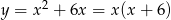 przesunięta o
przesunięta o  jednostek wzdłuż osi
jednostek wzdłuż osi 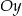 . Wierzchołek paraboli
. Wierzchołek paraboli 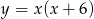 jest dokładnie między pierwiastkami, czyli w punkcie
jest dokładnie między pierwiastkami, czyli w punkcie
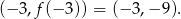
Jeżeli to naszkicujemy, to widać, że parabola przestanie przecinać oś 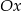 dla
dla 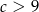 .
.
Odpowiedź: B

