Zadanie nr 3319460
Dany jest trójkąt o bokach długości 4, 5 oraz 6. Cosinus największego kąta wewnętrznego tego trójkąta jest równy
A) 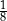 B)
B) 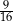 C)
C)  D)
D) 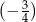
Rozwiązanie
Jak wiadomo, w trójkącie naprzeciwko większego kąta leży dłuższy bok. To oznacza, że interesuje nas cosinus kąta leżącego naprzeciwko boku długości 6.

Korzystamy oczywiście z twierdzenia cosinusów
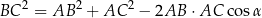
Mamy zatem
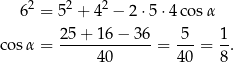
Odpowiedź: A

