Zadanie nr 6248181
Boki trójkąta mają długości 20 i 12, a kąt między tymi bokami ma miarę 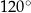 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 60 B) 120 C) 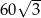 D)
D) 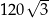
Rozwiązanie
Rozpoczynamy od rysunku.

Na mocy wzoru 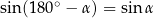 mamy
mamy
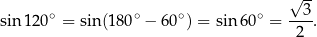
Ze wzoru na pole z sinusem mamy
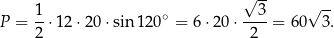
Odpowiedź: C

