Zadanie nr 6119833
Dany jest trójkąt prostokątny (patrz rysunek).
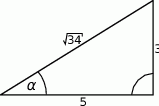
Wartość wyrażenia 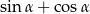 wynosi
wynosi
A) 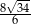 B)
B) 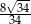 C)
C) 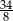 D) 1
D) 1
Rozwiązanie
Bezpośrednio z rysunku mamy
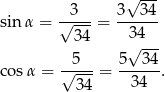
Zatem interesująca nas suma jest równa
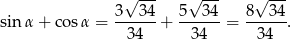
Odpowiedź: B
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trójkąt prostokątny (patrz rysunek).

Wartość wyrażenia 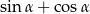 wynosi
wynosi
A) 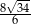 B)
B) 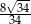 C)
C) 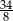 D) 1
D) 1
Bezpośrednio z rysunku mamy
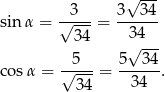
Zatem interesująca nas suma jest równa
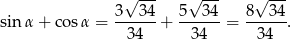
Odpowiedź: B
