Po dwukrotnej obniżce ceny za każdym razem o 4% buty kosztowały 230,40 zł. Ich cena początkowa to:
A) 250 zł B) 270 zł C) 290 zł D) 202,40 zł
/Szkoła średnia/Zadania testowe/Zadania z treścią
Cenę towaru dwukrotnie obniżano o 20%. W wyniku obniżek cena towaru wynosi 96 zł. Przed zmianami towar kosztował
A) 138,24 zł B) 144,00 zł C) 150,00 zł D) 160,00 zł
Cena działki po kolejnych dwóch obniżkach, za każdym razem o 10% w odniesieniu do ceny obowiązującej w danym momencie, jest równa 78 732 zł. Cena tej działki przed obiema obniżkami była, w zaokrągleniu do 1 zł, równa
A) 98 732 zł B) 97 200 zł C) 95 266 zł D) 94 478 zł
Po dwukrotnej obniżce, za każdym razem o 10% w stosunku do ceny obowiązującej w chwili obniżki, komputer kosztuje 1944 złote. Stąd wynika, że przed tymi obniżkami ten komputer kosztował
A) 2200 złotych. B) 2300 złotych. C) 2400 złotych. D) 3000 złotych.
Po dwukrotnej obniżce ceny za każdym razem o 6% kurtka kosztowała 220,90 zł. Jej cena początkowa to:
A) 248,20 zł B) 270 zł C) 290 zł D) 250 zł
Po dwukrotnej obniżce ceny, za każdym razem o 5%, kurtka kosztowała 245,48 zł. Jej cena początkowa to:
A) 270,64 zł B) 270 zł C) 272 zł D) 250 zł
Cenę samochodu, który początkowo kosztował 30000 zł dwukrotnie podniesiono o 10%, a następnie dwukrotnie obniżono o 10%. Po tych zmianach ceny samochód kosztował
A) 29403 B) 30000 C) 30597 D) 29700
Cenę aparatu, który początkowo kosztował 2000 zł dwukrotnie podniesiono o 10%, a następnie dwukrotnie obniżono o 10%. Po tych zmianach ceny aparat kosztował
A) 1620 zł B) 1960,2 zł C) 2000 zł D) 1980 zł
Czas trwania zabiegu rehabilitacyjnego wydłużono o 35% do 108 minut. Ile początkowo miał trwać ten zabieg?
A) 80 minut B) 90 minut C) 60 minut D) 70 minut
Piotrek ma w swojej bibliotece tylko książki historyczne i biograficzne. Książek historycznych ma 9, co stanowi 30% wszystkich jego książek. Wynika stąd, że liczba książek biograficznych Piotrka, to
A) 21 B) 30 C) 16 D) 10
Karol ma w swojej bibliotece tylko książki przyrodnicze i sensacyjne. Książek przyrodniczych ma 12, co stanowi 40% wszystkich jego książek. Wynika stąd, że liczba książek sensacyjnych Karola, to
A) 21 B) 18 C) 36 D) 24
Gienek ma w swojej bibliotece tylko książki przygodowe i historyczne. Książek historycznych ma 21, co stanowi 35% wszystkich jego książek. Wynika stąd, że liczba książek przygodowych Gienka, to
A) 21 B) 31 C) 39 D) 43
Samochód pokonał trasę długości 117 km w ciągu 39 minut. Gdyby samochód jadąc z tą samą prędkością średnią miał pokonać odległość 141 km, to zajęłoby to
A) 47 minut. B) 45 minut. C) 48 minut. D) 44 minuty.
Samochód pokonał trasę długości 115 km w ciągu 46 minut. Gdyby samochód jadąc z tą samą prędkością średnią miał pokonać odległość 240 km, to zajęłoby to
A) 94 minuty. B) 90 minut. C) 96 minut. D) 88 minut.
Pani Weronika wpłaciła do banku pewną kwotę na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank doliczał odsetki w wysokości 4% od kwoty bieżącego kapitału znajdującego się na lokacie. Po dwóch latach oszczędzania kapitał zgromadzony na lokacie (bez uwzględnienia podatków) był o 270,40 zł większy od kapitału zgromadzonego po roku oszczędzania. Kwota wpłacona przez panią Weronikę na tę lokatę była równa
A) 5800 zł B) 6500 zł C) 6400 zł D) 4800 zł
Na ścianie kamienicy zaprojektowano mural utworzony z szeregu trójkątów równobocznych różnej wielkości. Najmniejszy trójkąt ma bok długości 1 m, a bok każdego z następnych trójkątów jest o 10 cm dłuższy niż bok poprzedzającego go trójkąta. Ostatni trójkąt ma bok długości 5,9 m. Ile trójkątów przedstawia mural?
A) 49 B) 50 C) 59 D) 60
Na ścianie kamienicy zaprojektowano mural utworzony z szeregu trójkątów równobocznych różnej wielkości. Najmniejszy trójkąt ma bok długości 1 m, a bok każdego z następnych trójkątów jest o 15 cm dłuższy niż bok poprzedzającego go trójkąta. Ostatni trójkąt ma bok długości 6,4 m. Ile trójkątów przedstawia mural?
A) 35 B) 36 C) 37 D) 40
Samochód na pokonanie pierwszego odcinka trasy zużył 27 litrów benzyny. Na drugim odcinku trasy, mającym długość 150 km, zużył on dwa razy mniej benzyny niż na pierwszym odcinku. Średnie zużycie benzyny na kilometr było na każdym odcinku trasy takie samo. Średnie zużycie benzyny przez ten samochód na każde 100 km tej trasy było równe
A) 4,5 litra. B) 9 litrów. C) 13,5 litra. D) 18 litrów.
Samochód na pokonanie pierwszego odcinka trasy zużył 6,3 litra benzyny. Na drugim odcinku trasy, mającym długość 180 km, zużył on dwa razy więcej benzyny niż na pierwszym odcinku. Średnie zużycie benzyny na kilometr było na każdym odcinku trasy takie samo. Średnie zużycie benzyny przez ten samochód na każde 100 km tej trasy było równe
A) 7 litrów. B) 3,5 litra. C) 14 litrów. D) 4,2 litra.
Pan Nowak spłacił kredyt w 24 ratach. Pierwsza rata kredytu była równa 3000 zł, a każda następna była niższa od poprzedniej o 10%. Wysokość  -tej raty kredytu, gdzie
-tej raty kredytu, gdzie 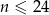 opisuje wzór:
opisuje wzór:
A) 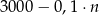 B)
B) 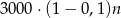 C)
C) 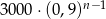 D)
D) 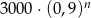
Pan Kowalski spłacił kredyt w 36 ratach. Pierwsza rata kredytu była równa 2000 zł, a każda następna była niższa od poprzedniej o 20%. Wysokość  -tej raty kredytu, gdzie
-tej raty kredytu, gdzie 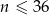 opisuje wzór:
opisuje wzór:
A) 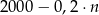 B)
B) 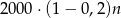 C)
C) 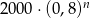 D)
D) 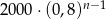
Pan Tadeusz spłacił kredyt w 12 ratach. Pierwsza rata kredytu była równa 1000 zł, a każda następna była wyższa od poprzedniej o 10%. Wysokość  -tej raty kredytu, gdzie
-tej raty kredytu, gdzie 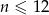 opisuje wzór:
opisuje wzór:
A) 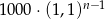 B)
B) 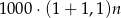 C)
C) 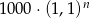 D)
D) 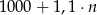
Do 200 ml soku dolano 0,3 litra wody. Stężenie soku w otrzymanym napoju jest równe
A) 66% B) 40% C) 150% D) 60%
Kubek ma kształt walca o wysokości 12 cm i promieniu podstawy 4 cm. Do kubka wypełnionego całkowicie wodą wpadła kulka o promieniu 3 cm i całkowicie się zanurzyła. Ile centymetrów sześciennych wody wylało się z kubka?
A) 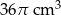 B)
B) 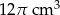 C)
C) 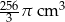 D)
D) 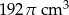
Kubek ma kształt walca o wysokości 11 cm i promieniu podstawy 5 cm. Do kubka wypełnionego całkowicie wodą wpadła kulka o promieniu 4 cm i całkowicie się zanurzyła. Ile centymetrów sześciennych wody wylało się z kubka?
A) 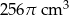 B)
B) 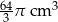 C)
C) 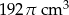 D)
D) 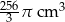
Szklanka ma kształt walca o wysokości 14 cm i promieniu podstawy 5 cm. Do szklanki wypełnionej całkowicie wodą wpadła kulka o promieniu 2 cm i całkowicie się zanurzyła. Ile centymetrów sześciennych wody wylało się ze szklanki?
A) 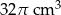 B)
B) 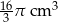 C)
C) 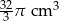 D)
D) 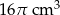
Zbiornik na wodę ma kształt prostopadłościanu o podstawie będącej prostokątem o bokach 5 m i 3 m, oraz o wysokości 4 metrów. Odległość między najdalszymi punktami zbiornika jest
A) większa niż 8 m B) większa niż 7 m i mniejsza niż 8 m
C) większa niż 6 m i mniejsza niż 7 m D) większa niż 5 m i mniejsza niż 6 m
W pewnym banku oprocentowanie kredytu konsumpcyjnego przez cały marzec było równe 17%. Na początku kwietnia podwyższono oprocentowanie tego kredytu o 3 punkty procentowe, a na początku maja obniżono o 4 punkty procentowe. Oznacza to, że oprocentowanie tego kredytu konsumpcyjnego między kwietniem a majem zmalało o
A) 5% B) 3% C) 25% D) 20%
Pole powierzchni jednej ze ścian ołowianej kostki do gry jest równe 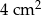 . Gęstość ołowiu jest równa ok.
. Gęstość ołowiu jest równa ok. 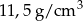 . Masa kostki jest równa około
. Masa kostki jest równa około
A) 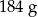 B)
B) 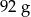 C)
C) 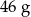 D)
D) 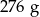
Pole powierzchni jednej ze ścian aluminiowej kostki do gry jest równe 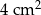 . Gęstość aluminium jest równa ok.
. Gęstość aluminium jest równa ok. 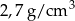 . Masa kostki jest równa około
. Masa kostki jest równa około
A) 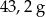 B)
B) 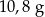 C)
C) 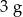 D)
D) 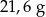
Pole powierzchni jednej ze ścian stalowej kostki do gry jest równe 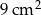 . Gęstość stali jest równa ok.
. Gęstość stali jest równa ok. 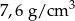 . Masa kostki jest równa około
. Masa kostki jest równa około
A) 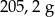 B)
B) 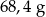 C)
C) 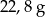 D)
D) 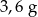
W pewnym sklepie ceny wszystkich płyt CD obniżono o 20%. Zatem za dwie płyty kupione w tym sklepie należy zapłacić mniej o
A) 10% B) 20% C) 30% D) 40%
Ile procent doby stanowi 15 minut?
A) około 1% B) 4% C) około 2% D) 12,5%
Karolina ma o 25% wyższy wynik z egzaminu próbnego od Oli. Wynika z tego, że Oli wynik jest niższy od wyniku Karoliny o
A) 25% B) 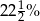 C) 20% D)
C) 20% D) 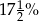
W klasie Ia jest o 25% więcej uczniów niż w klasie Ib. Stąd wynika, że w klasie Ib jest mniej uczniów niż w klasie Ia o
A) 25% B) 75% C) 20% D) 50%
W słoiku w kształcie walca o średnicy 10 cm mieści się 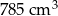 soku. Jeżeli przyjmiemy, że
soku. Jeżeli przyjmiemy, że 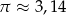 to wysokość słoika jest w przybliżeniu równa
to wysokość słoika jest w przybliżeniu równa
A) 2,5 cm B) 50 cm C) 25 cm D) 10 cm
W puszce w kształcie walca o średnicy 12 cm mieści się 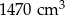 soku. Jeżeli przyjmiemy, że
soku. Jeżeli przyjmiemy, że 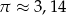 to wysokość puszki jest w przybliżeniu równa
to wysokość puszki jest w przybliżeniu równa
A) 13 cm B) 3,25 cm C) 26 cm D) 6,5 cm
W kubku w kształcie walca o średnicy 8 cm mieści się 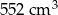 wody. Jeżeli przyjmiemy, że
wody. Jeżeli przyjmiemy, że 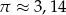 to wysokość kubka jest w przybliżeniu równa
to wysokość kubka jest w przybliżeniu równa
A) 2,7 cm B) 44 cm C) 11 cm D) 10 cm
Do pewnej liczby  dodano 54. Otrzymaną sumę podzielono przez 2. W wyniku tego działania otrzymano liczbę dwa razy większą od liczby
dodano 54. Otrzymaną sumę podzielono przez 2. W wyniku tego działania otrzymano liczbę dwa razy większą od liczby  . Zatem
. Zatem
A) 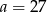 B)
B) 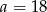 C)
C) 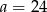 D)
D) 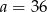
Do pewnej liczby  dodano 65. Otrzymaną sumę podzielono przez 2. W wyniku tego działania otrzymano liczbę trzy razy większą od liczby
dodano 65. Otrzymaną sumę podzielono przez 2. W wyniku tego działania otrzymano liczbę trzy razy większą od liczby  . Zatem
. Zatem
A) 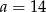 B)
B) 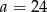 C)
C) 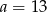 D)
D) 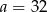
Liczba osobników pewnego zagrożonego wyginięciem gatunku zwierząt wzrosła w stosunku do liczby tych zwierząt z 31 grudnia 2011 r. o 120% i obecnie jest równa 8910. Ile zwierząt liczyła populacja tego gatunku w ostatnim dniu 2011 roku?
A) 4050 B) 1782 C) 7425 D) 7128
Liczba uczniów pewnej szkoły zmalała w stosunku do 1 września 2010 roku o 25% i obecenie jest równa 735. Ilu uczniów liczyła ta szkoła na początku roku szkolnego 2010/2011?
A) 551 B) 919 C) 980 D) 1050
Cena jednego bitcoina wzrosła w stosunku do ceny jednego bitcoina z dnia 1 stycznia 2017 o 1000% i wynosiła w grudniu 2017 roku 46860 zł. Jaka była cena jednego bitcoina w pierwszym dniu 2017 roku?
A) 4686 zł B) 527 zł C) 4260 zł D) 468 zł

