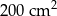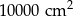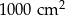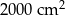Właściciel sklepu z zabawkami przeprowadził lokalne badanie rynkowe dotyczące wpływu zmiany ceny zestawu klocków na liczbę kupujących ten produkt. Z badania wynika, że dzienny przychód 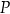 ze sprzedaży zestawów klocków, w zależności od kwoty obniżki ceny zestawu o
ze sprzedaży zestawów klocków, w zależności od kwoty obniżki ceny zestawu o  zł, wyraża się wzorem
zł, wyraża się wzorem
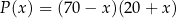
gdzie  jest liczbą całkowitą spełniającą warunki
jest liczbą całkowitą spełniającą warunki 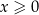 i
i 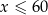 . Dzienny przychód ze sprzedaży zestawów klocków będzie równy 800 zł, gdy liczba
. Dzienny przychód ze sprzedaży zestawów klocków będzie równy 800 zł, gdy liczba  jest równa
jest równa
A) 25 B) 30 C) 45 D) 50 E) 60

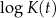 , gdzie
, gdzie 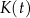 jest liczbą bakterii w próbce po czasie
jest liczbą bakterii w próbce po czasie 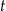 wyrażonym w godzinach, jaki upłynął od chwili
wyrażonym w godzinach, jaki upłynął od chwili 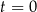 rozpoczęcia obserwacji.
rozpoczęcia obserwacji. 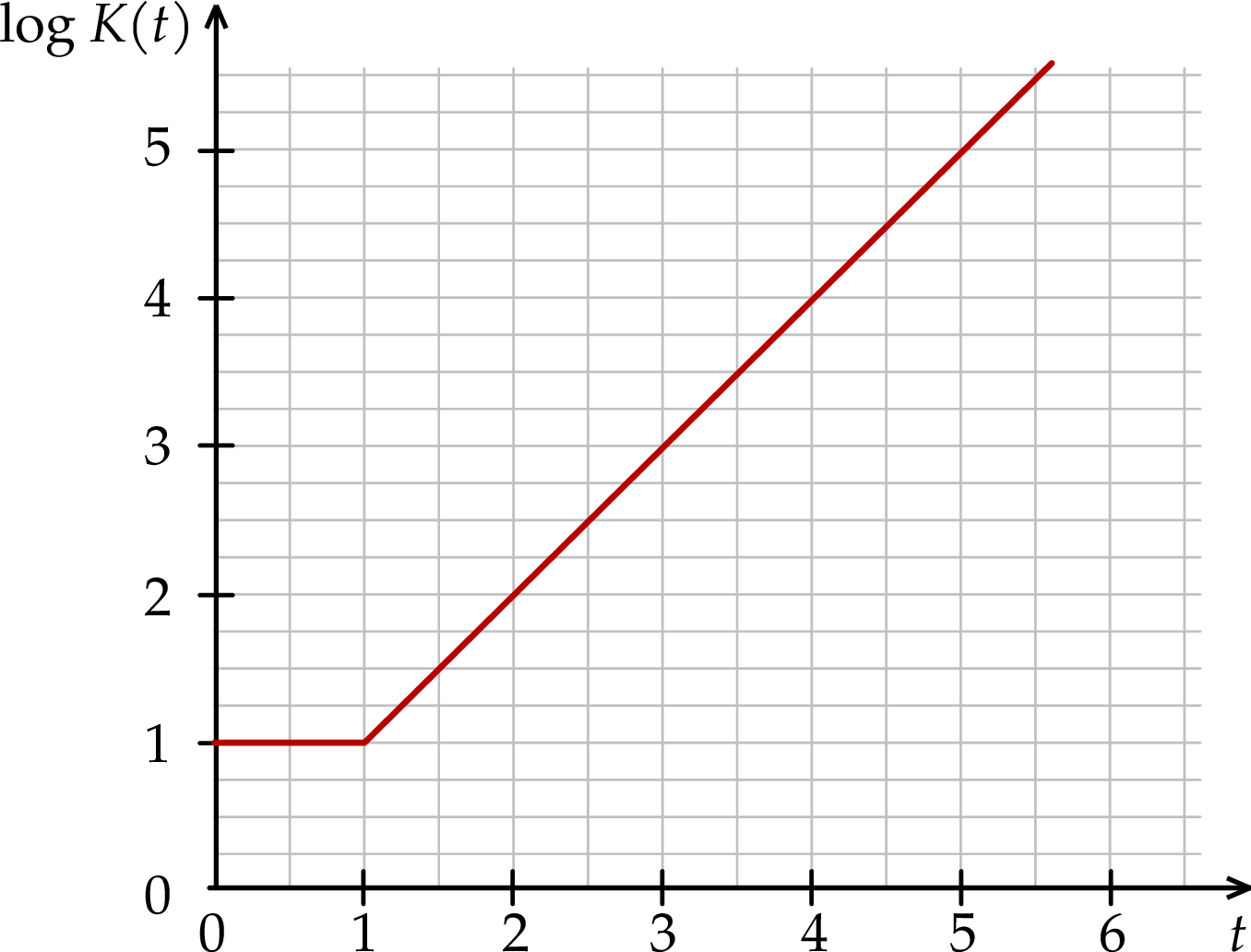
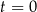 , liczba
, liczba 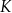 bakterii była równa
bakterii była równa 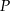 swojego produktu na liczbę
swojego produktu na liczbę 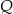 kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 1 jednostkę powoduje spadek liczby kupujących o 3 jednostki. Ponadto przy cenie równej 5 jednostek liczba kupujących jest równa 12 jednostek. Funkcja, która opisuje zależność liczby kupujących ten produkt od jego ceny, ma wzór
kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 1 jednostkę powoduje spadek liczby kupujących o 3 jednostki. Ponadto przy cenie równej 5 jednostek liczba kupujących jest równa 12 jednostek. Funkcja, która opisuje zależność liczby kupujących ten produkt od jego ceny, ma wzór 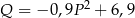
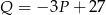
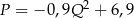
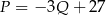
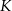 swojego produktu w zależności od liczby
swojego produktu w zależności od liczby 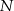 wyprodukowanych jednego dnia sztuk produktu. Z badań wynika, że każdorazowe zwiększenie dziennej produkcji o 10 sztuk produktu, powoduje wzrost dziennego kosztu produkcji o 15 jednostek. Ponadto, przy produkcji na poziomie 10 sztuk dziennie dzienny koszt produkcji jest równy 60 jednostek. Funkcja, która opisuje zależność dziennego kosztu produkcji przedmiotu od dziennej liczby produkowanych sztuk, ma wzór
wyprodukowanych jednego dnia sztuk produktu. Z badań wynika, że każdorazowe zwiększenie dziennej produkcji o 10 sztuk produktu, powoduje wzrost dziennego kosztu produkcji o 15 jednostek. Ponadto, przy produkcji na poziomie 10 sztuk dziennie dzienny koszt produkcji jest równy 60 jednostek. Funkcja, która opisuje zależność dziennego kosztu produkcji przedmiotu od dziennej liczby produkowanych sztuk, ma wzór 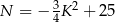
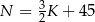
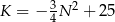
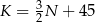
 godzin. Kasia i Ania postanowiły mu pomóc, przy czym każda z dziewczynek w ciągu jednej godziny wykonuje
godzin. Kasia i Ania postanowiły mu pomóc, przy czym każda z dziewczynek w ciągu jednej godziny wykonuje  pracy wykonanej w tym czasie przez Piotrka. Zatem wszystkie trzy osoby, pracując razem, ukończą pracę w ciągu
pracy wykonanej w tym czasie przez Piotrka. Zatem wszystkie trzy osoby, pracując razem, ukończą pracę w ciągu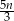 godzin
godzin 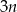 godzin
godzin 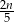 godzin
godzin 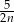 godzin
godzin  godzin. Zosia i Ela postanowiły mu pomóc, przy czym każda z pań w ciągu jednej godziny wykonuje
godzin. Zosia i Ela postanowiły mu pomóc, przy czym każda z pań w ciągu jednej godziny wykonuje  pracy wykonanej w tym czasie przez Wojtka. Zatem wszystkie trzy osoby, pracując razem, ukończą pracę w ciągu
pracy wykonanej w tym czasie przez Wojtka. Zatem wszystkie trzy osoby, pracując razem, ukończą pracę w ciągu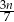 godzin
godzin 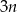 godzin
godzin 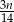 godzin
godzin 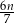 godzin
godzin  godzin. Małgosia i Ania postanowiły mu pomóc, przy czym każda z dziewczynek w ciągu jednej godziny wykonuje
godzin. Małgosia i Ania postanowiły mu pomóc, przy czym każda z dziewczynek w ciągu jednej godziny wykonuje  pracy wykonanej w tym czasie przez Janka. Zatem wszystkie trzy osoby, pracując razem, ukończą pracę w ciągu
pracy wykonanej w tym czasie przez Janka. Zatem wszystkie trzy osoby, pracując razem, ukończą pracę w ciągu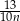 godzin
godzin 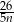 godzin
godzin 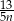 godzin
godzin 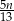 godzin
godzin  pewnego towaru dwukrotnie obniżono o 50% i otrzymano cenę
pewnego towaru dwukrotnie obniżono o 50% i otrzymano cenę 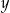 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 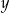 należy podnieść o
należy podnieść o  pewnego towaru dwukrotnie obniżono o 20% i otrzymano cenę
pewnego towaru dwukrotnie obniżono o 20% i otrzymano cenę 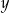 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 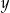 należy podnieść o
należy podnieść o 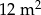 . Pole powierzchni tego pokoju na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tego pokoju na planie wykonanym w skali 1:200 wynosi: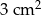
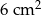
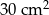
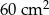
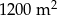 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi: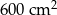
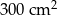
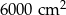
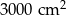
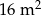 . Pole powierzchni tego pokoju na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tego pokoju na planie wykonanym w skali 1:200 wynosi: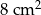
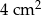
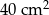
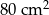
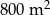 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi: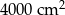
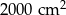
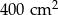
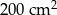
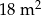 . Pole powierzchni tego pokoju na planie wykonanym w skali 1:300 wynosi:
. Pole powierzchni tego pokoju na planie wykonanym w skali 1:300 wynosi: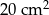
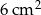
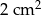
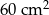
 przetopiono na metalowy walec o promieniu podstawy równym promieniowi kuli. Wysokość walca jest równa
przetopiono na metalowy walec o promieniu podstawy równym promieniowi kuli. Wysokość walca jest równa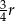
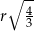
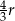
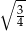
 i wysokości
i wysokości 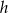 przetopiono na stożek o takim samym promieniu podstawy. Wysokość stożka jest równa
przetopiono na stożek o takim samym promieniu podstawy. Wysokość stożka jest równa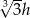
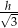

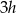
 przetopiono na metalowy stożek o promieniu podstawy równym promieniowi kuli. Wysokość stożka jest równa
przetopiono na metalowy stożek o promieniu podstawy równym promieniowi kuli. Wysokość stożka jest równa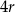
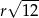
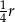
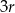
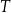 połowicznego rozpadu izotopu promieniotwórczego to czas, po którym liczba jąder danego izotopu (a zatem i masa tego izotopu) zmniejsza się o połowę – tzn. połowa jąder danego izotopu przemienia się w inne jądra. Liczba jąder
połowicznego rozpadu izotopu promieniotwórczego to czas, po którym liczba jąder danego izotopu (a zatem i masa tego izotopu) zmniejsza się o połowę – tzn. połowa jąder danego izotopu przemienia się w inne jądra. Liczba jąder 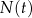 izotopu promieniotwórczego pozostających w próbce po czasie
izotopu promieniotwórczego pozostających w próbce po czasie 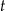 , licząc od chwili
, licząc od chwili 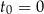 , wyraża się zależnością wykładniczą:
, wyraża się zależnością wykładniczą: 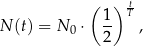
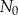 jest liczbą jąder izotopu promieniotwórczego w chwili początkowej
jest liczbą jąder izotopu promieniotwórczego w chwili początkowej 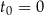 . Wykres zależności wykładniczej
. Wykres zależności wykładniczej 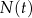 – opisanej we wstępie do zadania – przedstawiono na rysunku
– opisanej we wstępie do zadania – przedstawiono na rysunku 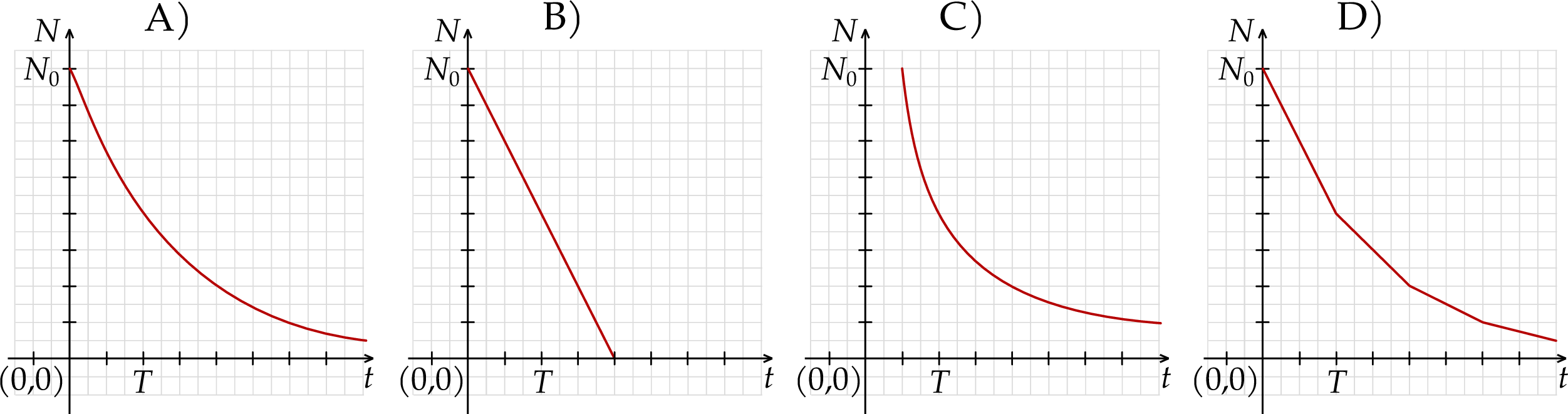
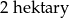 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi: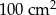
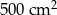
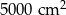
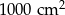
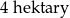 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi: