Zadanie nr 5610495
Dany jest trójkąt prostokątny 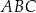 o bokach
o bokach 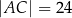 ,
, 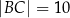 ,
, 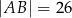 . Dwusieczne kątów tego trójkąta przecinają się w punkcie
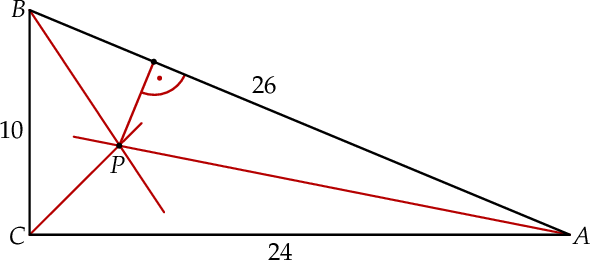
. Dwusieczne kątów tego trójkąta przecinają się w punkcie 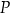 (zobacz rysunek).
(zobacz rysunek).
Odległość  punktu
punktu 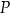 od przeciwprostokątnej
od przeciwprostokątnej 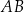 jest równa
jest równa
A) 2 B) 4 C)  D)
D) 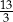
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

