Zadanie nr 4826245
Ciąg arytmetyczny 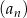 , określony dla
, określony dla 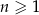 , spełnia warunek
, spełnia warunek 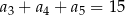 . Wtedy
. Wtedy
A) 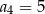 B)
B) 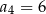 C)
C) 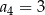 D)
D) 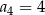
Rozwiązanie
Sposób I
Jeżeli oznaczymy przez  różnicę ciągu
różnicę ciągu 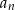 , to
, to
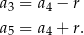
Zatem
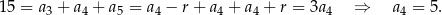
Sposób II
Ze wzoru 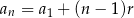 na
na  -ty wyraz ciągu arytmetycznego mamy
-ty wyraz ciągu arytmetycznego mamy
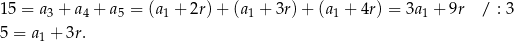
Zatem 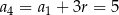 .
.
Odpowiedź: A

