Zadanie nr 8209067
Oblicz całkę 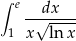 .
.
Rozwiązanie
Funkcja podcałkowa ma w przedziale ![[1,e]](https://img.zadania.info/zad/8209067/HzadR0x.gif) jeden punkt osobliwy
jeden punkt osobliwy 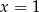 . Liczymy całkę nieoznaczoną
. Liczymy całkę nieoznaczoną
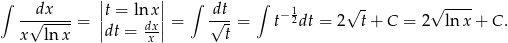
Zatem
![∫ e dx [ √ ---]e -√----- = 2 ln x = 2− 0 = 2. 1 x ln x 1](https://img.zadania.info/zad/8209067/HzadR3x.gif)
Odpowiedź: 2
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 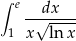 .
.
Funkcja podcałkowa ma w przedziale ![[1,e]](https://img.zadania.info/zad/8209067/HzadR0x.gif) jeden punkt osobliwy
jeden punkt osobliwy 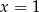 . Liczymy całkę nieoznaczoną
. Liczymy całkę nieoznaczoną
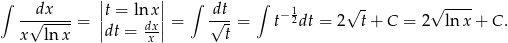
Zatem
![∫ e dx [ √ ---]e -√----- = 2 ln x = 2− 0 = 2. 1 x ln x 1](https://img.zadania.info/zad/8209067/HzadR3x.gif)
Odpowiedź: 2
