Zadanie nr 8732542
Punkty 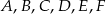 są kolejnymi wierzchołkami sześciokąta foremnego, przy czym
są kolejnymi wierzchołkami sześciokąta foremnego, przy czym 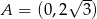 ,
, 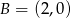 , a
, a 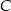 leży na osi
leży na osi 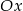 . Wyznacz równanie stycznej do okręgu opisanego na tym sześciokącie przechodzącej przez wierzchołek
. Wyznacz równanie stycznej do okręgu opisanego na tym sześciokącie przechodzącej przez wierzchołek 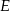 .
.
Rozwiązanie
Zauważmy najpierw, że znając współrzędne dwóch kolejnych wierzchołków sześciokąta, możemy obliczyć długość jego boku.
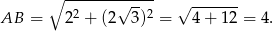
W takim razie 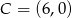 i możemy naszkicować opisaną sytuację.
i możemy naszkicować opisaną sytuację.
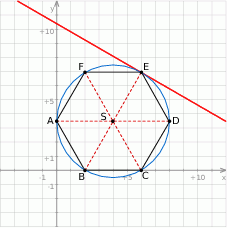
Sześciokąt foremny skład się z 6 przystających trójkątów równobocznych o wspólnym wierzchołku w środku 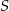 sześciokąta. Współrzędne punktu
sześciokąta. Współrzędne punktu 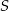 łatwo wyznaczyć: jego druga współrzędna jest taka sama jak druga współrzędna punktu
łatwo wyznaczyć: jego druga współrzędna jest taka sama jak druga współrzędna punktu 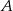 , a pierwsza jest równa 4 (bo prosta
, a pierwsza jest równa 4 (bo prosta 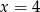 jest osią symetrii sześciokąta). Zatem
jest osią symetrii sześciokąta). Zatem 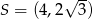 . To z kolei pozwala wyznaczyć współrzędne punktu
. To z kolei pozwala wyznaczyć współrzędne punktu 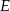 .
.
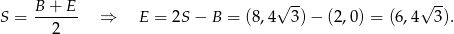
Szukana styczna jest prostopadła do promienia 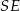 , więc jest równoległa do prostej
, więc jest równoległa do prostej 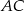 . Wyznaczmy współczynnik kierunkowy prostej
. Wyznaczmy współczynnik kierunkowy prostej 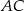 . Szukamy prostej
. Szukamy prostej 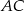 w postaci
w postaci 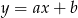 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 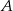 i
i 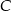 .
.
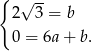
Stąd
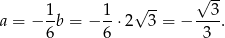
Szukana styczna ma ten sam współczynnik kierunkowy i przechodzi przez punkt 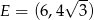 . Jest to więc prosta
. Jest to więc prosta
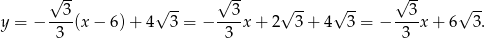
Odpowiedź: