/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Ekstrema/Z logarytmem

Zadanie nr 1630117

Wyznacz ekstrema lokalne funkcji 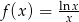lnx f (x) = x .

Rozwiązanie

Ze względu na logarytm musimy mieć oczywiście 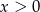x > 0 . Liczymy pochodną

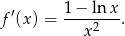
f ′(x ) = 1-−-lnx-. x2

Mianownik jest dodatni, więc pochodna zmienia znak z dodatniego na ujemny przechodząc przez punkt 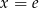x = e . To oznacza, że w tym punkcie funkcja ma maksimum lokalne. Wartość funkcji w tym punkcie to

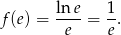
ln-e 1- f(e) = e = e .

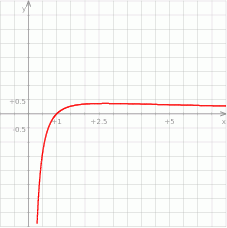
Na koniec obrazek.

Odpowiedź: Maksimum lokalne: 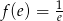f(e) = 1e .

Wersja PDF