Walec i stożek mają równe promienie podstaw, a wysokość walca jest dwa razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 3 B) 6 C) 2 D) 12
/Szkoła średnia/Zadania testowe/Geometria/Stereometria/Walec/Objętość
Walec i stożek mają równe promienie podstaw, a wysokość walca jest trzy razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 9 B) 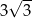 C) 3 D) 27
C) 3 D) 27
Prostokąt o bokach 4 i 6 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 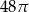 B)
B) 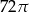 C)
C) 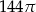 D)
D) 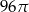
Prostokąt o bokach 10 i 6 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 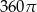 B)
B) 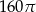 C)
C) 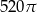 D)
D) 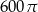
Prostokąt o bokach 3 i 5 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 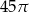 B)
B) 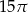 C)
C) 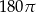 D)
D) 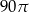
Pole powierzchni bocznej walca jest równe 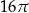 , a promień jego podstawy ma długość 2. Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych. Objętość tego walca jest równa A) 16 B) 32 C)
, a promień jego podstawy ma długość 2. Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych. Objętość tego walca jest równa A) 16 B) 32 C) 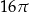 D)
D) 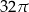
Objętość walca o promieniu podstawy  i wysokości 2 razy większej od promienia jest równa
i wysokości 2 razy większej od promienia jest równa
A) 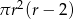 B)
B) 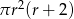 C)
C) 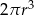 D)
D) 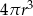
Objętość walca o promieniu podstawy  i wysokości 4 razy mniejszej od promienia jest równa
i wysokości 4 razy mniejszej od promienia jest równa
A) 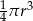 B)
B) 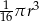 C)
C) 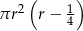 D)
D) 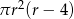
Objętość walca o promieniu podstawy  i wysokości 3 razy większej od promienia jest równa
i wysokości 3 razy większej od promienia jest równa
A) 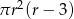 B)
B) 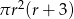 C)
C) 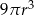 D)
D) 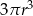
Objętość walca o promieniu podstawy  i wysokości 2 razy mniejszej od promienia jest równa
i wysokości 2 razy mniejszej od promienia jest równa
A) 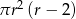 B)
B) 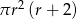 C)
C) 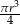 D)
D) 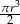
Dany jest walec, w którym promień podstawy jest równy  , a wysokość walca jest od tego promienia o dwa większa. Objętość tego walca jest równa
, a wysokość walca jest od tego promienia o dwa większa. Objętość tego walca jest równa
A) 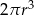 B)
B) 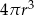 C)
C) 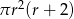 D)
D) 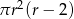
Dany jest walec, w którym promień podstawy jest równy  , a wysokość walca jest od tego promienia dwa razy większa. Objętość tego walca jest równa
, a wysokość walca jest od tego promienia dwa razy większa. Objętość tego walca jest równa
A) 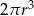 B)
B) 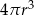 C)
C) 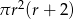 D)
D) 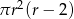
Przekrojem osiowym walca jest kwadrat o przekątnej długości 12. Objętość tego walca jest zatem równa
A) 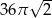 B)
B) 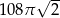 C)
C) 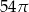 D)
D) 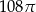
Przekrojem osiowym walca jest kwadrat o przekątnej długości 16. Objętość tego walca jest zatem równa
A) 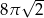 B)
B) 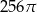 C)
C) 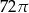 D)
D) 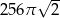
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 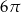 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 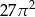 B)
B) 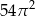 C)
C) 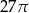 D)
D) 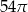
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 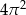 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 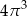 B)
B) 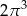 C)
C) 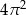 D)
D) 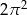
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 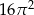 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 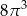 B)
B) 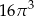 C)
C) 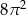 D)
D) 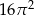
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 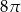 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 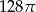 B)
B) 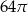 C)
C) 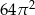 D)
D) 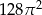
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 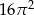 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 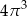 B)
B) 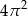 C)
C) 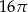 D)
D) 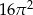
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
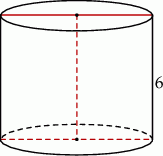
A) 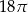 B)
B) 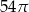 C)
C) 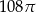 D)
D) 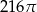
Przekrój osiowy walca jest kwadratem o boku 10. Objętość tego walca jest równa
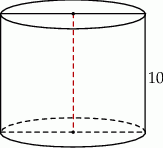
A) 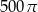 B)
B) 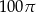 C)
C) 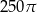 D)
D) 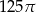
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
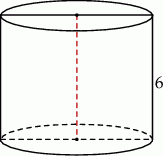
A) 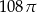 B)
B) 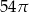 C)
C) 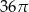 D)
D) 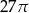
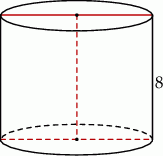
Przekrój osiowy walca jest kwadratem o boku długości 8. Objętość tego walca jest równa
A) 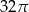 B)
B) 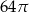 C)
C) 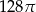 D)
D) 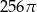
Jeżeli przekrój osiowy walca jest kwadratem o boku 4, to objętość walca jest równa
A) 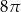 B)
B) 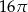 C)
C) 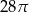 D)
D) 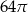
Promień podstawy walca zwiększamy trzy razy, a jego wysokość zmniejszamy trzy razy. Wówczas objętość walca
A) zwiększy się trzy razy B) zmniejszy się trzy razy
C) zwiększy się o trzy D) nie zmieni się
Promień podstawy walca zwiększamy cztery razy, a jego wysokość zmniejszamy cztery razy. Wówczas objętość walca
A) nie zmieni się B) zwiększy się o cztery
C) zmniejszy się cztery razy D) zwiększy się cztery razy
Promień podstawy walca zmniejszamy trzy razy, a jego wysokość zwiększamy trzy razy. Wówczas objętość walca
A) zwiększy się trzy razy B) zmniejszy się trzy razy
C) zwiększy się o trzy D) nie zmieni się

