Zadanie nr 6281590
W trapezie 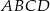 ramiona mają długości
ramiona mają długości 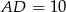 oraz
oraz 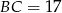 , zaś tangens kąta nachylenia ramienia
, zaś tangens kąta nachylenia ramienia 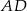 do dłuższej podstawy
do dłuższej podstawy 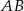 wynosi
wynosi 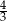 . Wiedząc, że w dany trapez można wpisać okrąg oblicz
. Wiedząc, że w dany trapez można wpisać okrąg oblicz
- pole trapezu,
- pole trójkąta
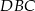 .
.
Rozwiązanie
Narysujmy opisaną sytuację.
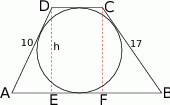
- Ponieważ trapez jest opisany na okręgu, więc sumy przeciwległych boków są równe, są one więc równe
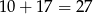 . Skoro znamy sumę podstaw, to do wyliczenia pola trapezu potrzebna nam jest już tylko wysokość
. Skoro znamy sumę podstaw, to do wyliczenia pola trapezu potrzebna nam jest już tylko wysokość 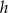 . Z podanej informacji o tangensie kąta
. Z podanej informacji o tangensie kąta 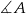 , mamy
, mamy 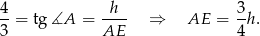
Stosujemy teraz twierdzenie Pitagorasa w trójkącie
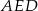
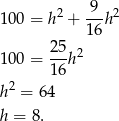
Stąd szukane pole
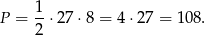
Odpowiedź: 108 - Aby wyliczyć pole trójkąta
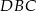 musimy się trochę bardziej wysilić, bo potrzebujemy długość podstawy
musimy się trochę bardziej wysilić, bo potrzebujemy długość podstawy 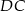 . Z twierdzenia Pitagorasa wyliczamy długości odcinków
. Z twierdzenia Pitagorasa wyliczamy długości odcinków 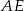 i
i 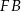 .
. 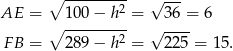
Stąd
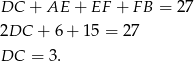
Zatem
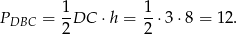
Odpowiedź: 12

