Zadanie nr 2811896
Trójkąt prostokątny 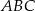 ma boki długości 3, 4, 5. Oblicz promień okręgu stycznego do przeciwprostokątnej i prostych będących przedłużeniami przyprostokątnych.
ma boki długości 3, 4, 5. Oblicz promień okręgu stycznego do przeciwprostokątnej i prostych będących przedłużeniami przyprostokątnych.
Rozwiązanie
Zaczynamy od rysunku.
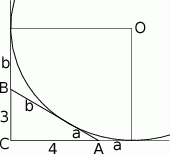
Jeżeli połączymy środek okręgu dopisanego do boku 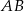 , to otrzymamy kwadrat o boku równym szukanemu promieniowi. Oznaczymy długości odcinków łączących punkty
, to otrzymamy kwadrat o boku równym szukanemu promieniowi. Oznaczymy długości odcinków łączących punkty 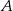 i
i 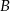 z punktami styczności okręgu i prostych zawierających boki trójkąta przez
z punktami styczności okręgu i prostych zawierających boki trójkąta przez  i
i 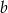 . Oczywiście wystarczy obliczyć
. Oczywiście wystarczy obliczyć  lub
lub 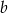 . Mamy układ równań
. Mamy układ równań
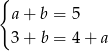
Podstawiając do drugiego równania za  z pierwszego mamy
z pierwszego mamy
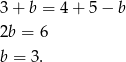
Zatem szukany promień ma długość 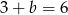 .
.
Odpowiedź: 6

