Zadanie nr 5353985
Przez początek układu współrzędnych poprowadzono prostą przecinającą okrąg 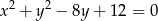 w dwóch punktach
w dwóch punktach 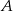 i
i 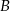 . Uzasadnij, że liczba
. Uzasadnij, że liczba  nie zależy od wyboru prostej i oblicz wartość tego iloczynu.
nie zależy od wyboru prostej i oblicz wartość tego iloczynu.
Rozwiązanie
Przekształćmy na początek podane równanie okręgu.
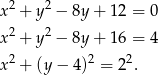
Jest to więc okrąg o środku w punkcie 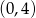 i promieniu 2. Możemy teraz narysować opisaną sytuację.
i promieniu 2. Możemy teraz narysować opisaną sytuację.
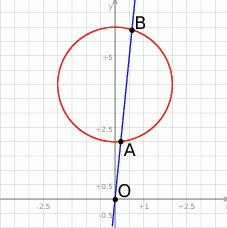
Proste przechodzące przez początek układu możemy zapisać w postaci 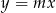 . Ta postać ma jednak wadę, bo nie uwzględnia pionowej prostej
. Ta postać ma jednak wadę, bo nie uwzględnia pionowej prostej 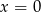 . Dlatego lepiej jest te proste sparametryzować wzorem
. Dlatego lepiej jest te proste sparametryzować wzorem 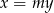 (teraz też nie ma jednej prostej:
(teraz też nie ma jednej prostej: 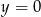 , ale ona nie przecina okręgu). Szukamy punktów wspólnych takiej prostej i okręgu.
, ale ona nie przecina okręgu). Szukamy punktów wspólnych takiej prostej i okręgu.
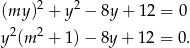
Zanim zajmiemy się tym równaniem, zobaczmy co mamy wyliczyć. Jeżeli 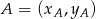 i
i 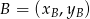 to mamy wyliczyć
to mamy wyliczyć
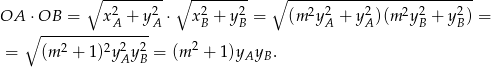
Opuściliśmy pierwiastek, bo z rysunku jest jasne, że 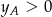 i
i 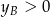 (wszystkie punkty okręgu mają tę własność). Możemy więc obliczyć szukany iloczyn ze wzorów Viète’a.
(wszystkie punkty okręgu mają tę własność). Możemy więc obliczyć szukany iloczyn ze wzorów Viète’a.
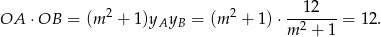
Zauważmy, że nie musimy sprawdzać, kiedy otrzymane równanie kwadratowe ma pierwiastki – my zakładamy, że je ma (co jakoś tam przekłada się na 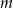 ) i badamy ich własności.
) i badamy ich własności.
Dla ciekawskich. Zadanie jest szczególnym przypadkiem tzw. twierdzenia o siecznej: jeżeli przez punkt 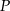 poprowadzimy sieczną okręgu o środku
poprowadzimy sieczną okręgu o środku 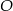 i promieniu
i promieniu  , która przecina ten okrąg w punktach
, która przecina ten okrąg w punktach 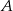 i
i 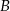 , to
, to
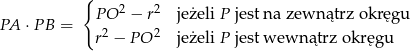
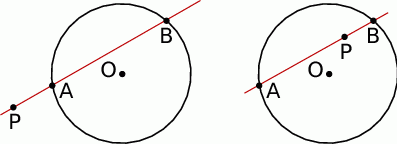
W szczególności iloczyn ten nie zależy od wyboru siecznej (może też być styczna, wtedy 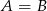 ). Twierdzenie to nosi też nazwę twierdzenia o potędze punktu względem okręgu – można sobie to wygooglać.
). Twierdzenie to nosi też nazwę twierdzenia o potędze punktu względem okręgu – można sobie to wygooglać.
Odpowiedź: 12

