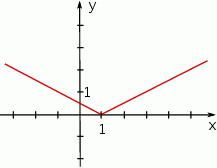
Dla jakich argumentów funkcja przedstawiona na wykresie przyjmuje wartość 1?
A) tylko dla argumentu 3 B) dla argumentów 0 i 2
C) dla argumentów 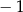 i 3 D) tylko dla argumentu
i 3 D) tylko dla argumentu 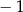
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dla jakich argumentów funkcja przedstawiona na wykresie przyjmuje wartość 1?

A) tylko dla argumentu 3 B) dla argumentów 0 i 2
C) dla argumentów 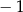 i 3 D) tylko dla argumentu
i 3 D) tylko dla argumentu 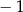
Dla jakich argumentów funkcja przedstawiona na wykresie przyjmuje wartość 3?
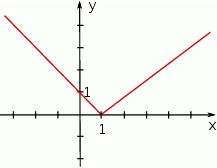
A) tylko dla argumentu 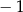 B) dla argumentów
B) dla argumentów 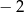 i 5
i 5
C) dla argumentów 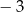 i 4 D) tylko dla argumentu 5
i 4 D) tylko dla argumentu 5
Dla jakich argumentów funkcja przedstawiona na wykresie przyjmuje wartość 2?
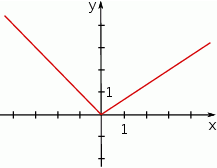
A) tylko dla argumentu 1 B) tylko dla argumentu 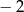
C) dla argumentów 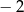 i 1 D) dla argumentów
i 1 D) dla argumentów 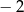 i 3
i 3
Cena brutto = cena netto + podatek VAT
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli cena netto 1 kg jabłek jest równa 2,50 zł, a cena brutto jest równa 2,70 zł, to podatek VAT wynosi 8% ceny netto. | P | F |
| Jeżeli cena netto podręcznika do matematyki jest równa 22 zł, to cena tej książki z 5% podatkiem VAT wynosi 24,10 zł. | P | F |
Cena brutto = cena netto + podatek VAT
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli cena netto laptopa jest równa 1200 zł, a cena brutto jest równa 1440 zł, to podatek VAT wynosi 22% ceny netto. | P | F |
| Jeżeli cena netto myszki komputerowej jest równa 36 zł, to cena tej myszki z 20% podatkiem VAT wynosi 43,20 zł. | P | F |
Na diagramie przedstawiono wielkość produkcji krzeseł w firmie Mebelix w 2015 r. i 2016 r.
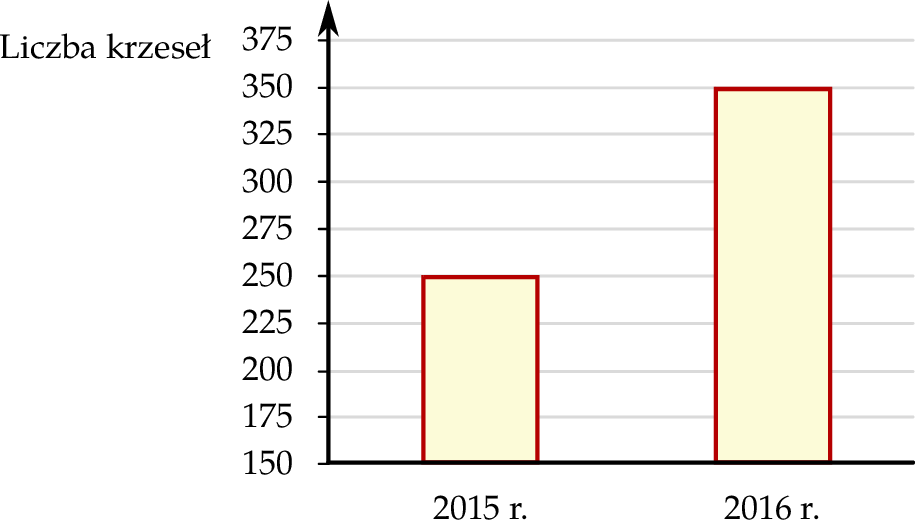
Czy liczba wyprodukowanych krzeseł w roku 2016 była o 100% większa od liczby wyprodukowanych krzeseł w roku 2015? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | drugi słupek na wykresie jest 2 razy wyższy od pierwszego. |
| B) | liczba krzeseł wyprodukowanych w 2016 roku jest o 40% większa niż liczba krzeseł wyprodukowanych w 2015 roku. |
| C) | w roku 2016 wyprodukowano o 250 krzeseł więcej niż w roku 2015. |
Średnia arytmetyczna trzech liczb: 12, 14, 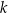 , jest równa 16. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, jest równa 16. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 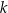 jest równa 22. jest równa 22. | P | F |
Średnia arytmetyczna liczb: 12, 14, 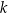 , 11, 17, jest większa od 16. , 11, 17, jest większa od 16. | P | F |
Na diagramie przedstawiono liczbę uczniów z podziałem na płeć w czterech klasach pewnej szkoły.
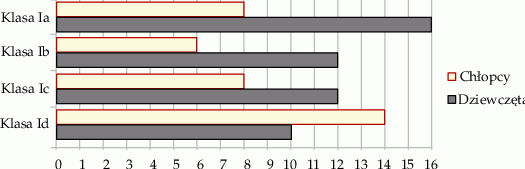
Czy wylosowanie dziewczynki jest bardziej prawdopodobne w klasie Ia, niż w każdej z trzech pozostałych klas? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w klasie Ia jest więcej dziewcząt, niż w każdej z pozostałych klas. |
| B) | stosunek liczby dziewcząt do liczby chłopców jest największy w klasie Ia. |
| C) | stosunek liczby dziewcząt do liczby chłopców jest taki sam w klasie Ia jak w jednej z pozostałych klas. |
Na diagramie przedstawiono liczbę uczniów z podziałem na płeć w czterech klasach pewnej szkoły.
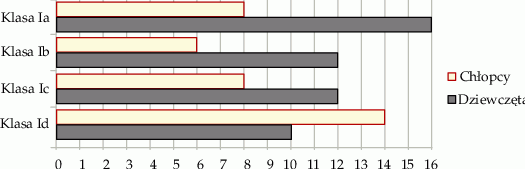
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wylosowania chłopca z klasy Id jest większe niż prawdopodobieństwo wylosowania dziewczynki wśród uczniów uczęszczających do pozostałych klas. | P | F |
Prawdopodobieństwo wylosowania chłopca z klasy Ic jest równe 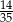 | P | F |
Piechur szedł z punktu 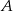 do punktu
do punktu 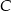 ze stałą prędkością. Część trasy przeszedł wzdłuż prostej, a część – po łuku okręgu o środku w punkcie
ze stałą prędkością. Część trasy przeszedł wzdłuż prostej, a część – po łuku okręgu o środku w punkcie 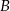 (patrz rysunek).
(patrz rysunek).
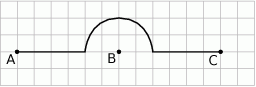
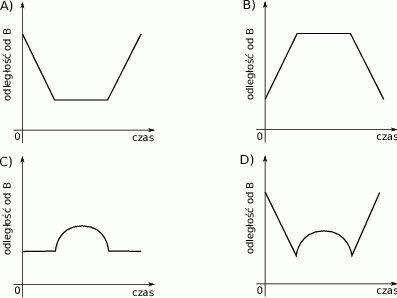
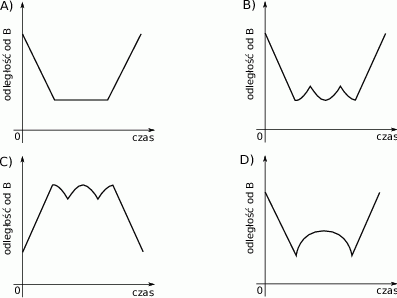
Na którym z poniższych wykresów zilustrowano, jak zmieniała się odległość piechura od punktu B?
Piechur szedł z punktu 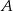 do punktu
do punktu 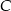 ze stałą prędkością. Na rysunku przedstawiono kształt trasy po jakiej się poruszał.
ze stałą prędkością. Na rysunku przedstawiono kształt trasy po jakiej się poruszał.
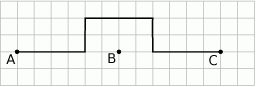
Na którym z poniższych wykresów zilustrowano, jak zmieniała się odległość piechura od punktu B?
Na diagramie przedstawiono wyniki pracy klasowej z matematyki w pewnej klasie.
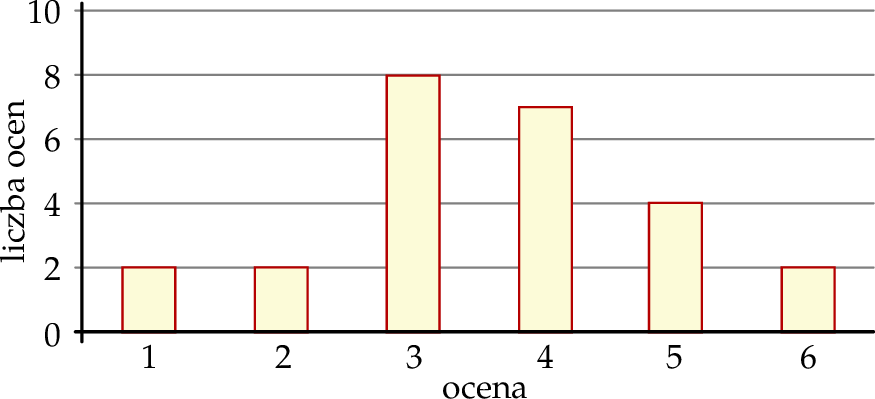
Z informacji podanych na diagramie wynika, że
A) pracę klasową pisało 30 uczniów.
B) najczęściej powtarzającą się oceną jest 4.
C) mediana wyników z pracy klasowej wynosi 2.
D) średnia wyników z pracy klasowej jest równa 3,6.
Na diagramie przedstawiono wysokość miesięcznych zarobków wszystkich pracowników pewnej firmy.
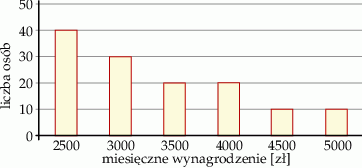
Z informacji podanych na diagramie wynika, że
A) w tej firmie pracuje 120 osób.
B) mediana miesięcznych zarobków wynosi 3250 zł.
C) średnia miesięcznych zarobków jest równa 3500 zł.
D) ponad połowa pracowników zarabia miesięcznie mniej niż 3500 zł.
Na diagramie przedstawiono wyniki pracy klasowej z matematyki w pewnej klasie.
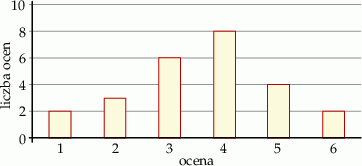
Z informacji podanych na diagramie wynika, że
A) pracę klasową pisało 24 uczniów.
B) najczęściej powtarzającą się oceną jest 3.
C) mediana wyników z pracy klasowej wynosi 4.
D) średnia wyników z pracy klasowej jest równa 3,5.
Tomek ma do dyspozycji 6 kartoników z literami: I, V, D, L, M, X (zobacz rysunek) i układa z nich różne liczby zapisane w systemie rzymskim, przy czym za każdym razem używa wszystkich sześciu kartoników.
![]()
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Największa liczba jaką może ułożyć Tomek to 1666. | P | F |
| Najmniejsza liczba jaką może ułożyć Tomek to 1544. | P | F |
Z prostokąta 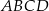 o polu 30 wycięto trójkąt
o polu 30 wycięto trójkąt 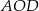 (tak jak na rysunku). Pole zacieniowanej figury jest równe
(tak jak na rysunku). Pole zacieniowanej figury jest równe
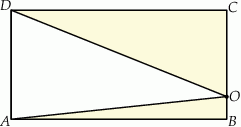
A) 7,5 B) 15 C) 20 D) 25
Z prostokąta 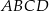 o polu 28 wycięto trójkąt
o polu 28 wycięto trójkąt 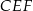 , przy czym punkty
, przy czym punkty 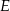 i
i 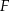 są środkami odpowiednio boków
są środkami odpowiednio boków 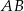 i
i 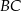 .
.
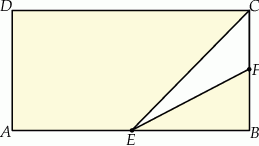
Pole zacieniowanej figury jest równe
A) 3,5 B) 21 C) 25 D) 24,5
O godzinie 14:50 Maciek wyruszył w podróż pociągiem z Gdańska do Grudziądza. Najpierw dojechał do Iławy, gdzie po 50–minutowym oczekiwaniu wsiadł do pociągu, którym dojechał do Grudziądza. Na rysunku pokazano, jak w czasie przebiegała podróż Maćka. Na osi czas przejazdu z Gdańska do Grudziądza podzielono na 20 jednakowych odstępów.
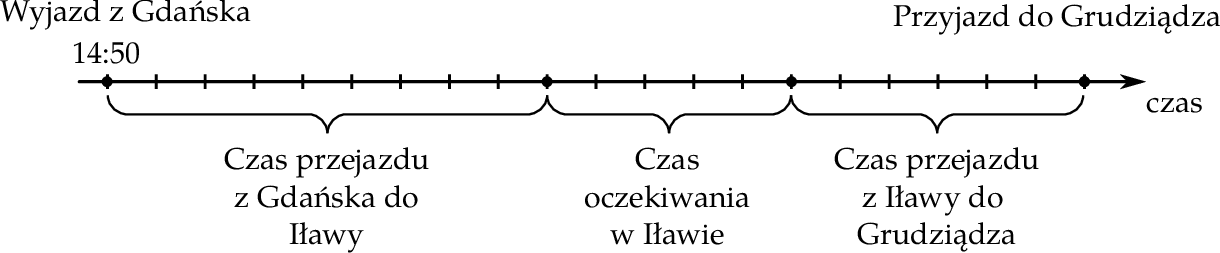
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przejazd z Iławy do Grudziądza trwał jedną godzinę. | P | F |
| Maciek przyjechał do Grudziądza o godzinie 18:10. | P | F |
O godzinie 18:50 Zbyszek wyruszył w podróż pociągiem z Poznania do Legnicy. Najpierw dojechał do Wrocławia, gdzie po 50–minutowym oczekiwaniu wsiadł do pociągu, którym dojechał do Legnicy. Na rysunku pokazano, jak w czasie przebiegała podróż Zbyszka. Na osi czas przejazdu z Poznania do Legnicy podzielono na 22 jednakowe odstępy.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przejazd z Poznania do Wrocławia trwał dwie godziny. | P | F |
| Zbyszek przyjechał do Legnicy o godzinie 21:30. | P | F |
O godzinie 10:50 Magda wyruszyła w podróż pociągiem z Krakowa do Żywca. Najpierw dojechała do Katowic, gdzie miała przesiadkę na pociąg do Żywca. Do Źywca dojechała o godzinie 13:35. Na rysunku pokazano, jak w czasie przebiegała podróż Magdy. Na osi czas przejazdu z Krakowa do Żywca podzielono na jednakowe odstępy.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Magda dojechała do Katowic o godzinie 11:35. | P | F |
| Czas oczekiwania na pociąg w Katowicach stanowił mniej niż 20% całego czasu podróży. | P | F |
W równoległoboku 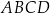 bok
bok 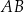 jest dwa razy dłuższy od boku
jest dwa razy dłuższy od boku 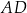 . Punkt
. Punkt 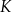 jest środkiem boku
jest środkiem boku 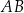 , a punkt
, a punkt 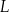 jest środkiem boku
jest środkiem boku 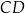 .
.
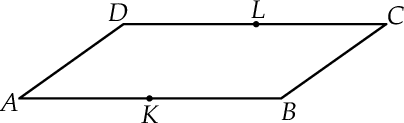
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 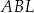 ma takie samo pole, jak trójkąt ma takie samo pole, jak trójkąt 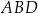 . . | P | F |
Pole równoległoboku 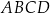 jest cztery razy większe od pola trójkąta jest cztery razy większe od pola trójkąta 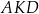 . . | P | F |
W równoległoboku 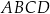 bok
bok 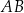 jest dwa razy dłuższy od boku
jest dwa razy dłuższy od boku 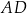 . Punkt
. Punkt 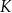 jest środkiem boku
jest środkiem boku 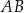 , a punkt
, a punkt 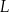 jest środkiem boku
jest środkiem boku 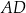 .
.
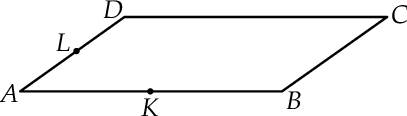
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 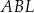 ma takie samo pole, jak trójkąt ma takie samo pole, jak trójkąt 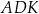 . . | P | F |
Pole równoległoboku 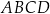 jest cztery razy większe od pola trójkąta jest cztery razy większe od pola trójkąta 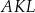 . . | P | F |
Piechur porusza się z prędkością 4 km/h. Każdy jego krok ma długość 0,8 m.
Ile kroków wykona piechur w czasie 12 minut?
A) 1000 kroków B) 800 kroków C) 640 kroków D) 100 kroków
Piechur porusza się z prędkością 5 km/h. Każdy jego krok ma długość 62,5 cm.
Ile kroków wykona piechur w czasie 15 minut?
A) 1000 kroków B) 2000 kroków C) 200 kroków D) 100 kroków
Zając porusza się z prędkością 40 km/h wykonując skoki długości 80 cm.
Ile skoków wykona zając w czasie 9 minut?
A) 1000 skoków B) 7500 skoków C) 6400 skoków D) 2000 skoków
Maszyna pakująca pakuje przyprawę w 200 gramowe saszetki z prędkością 2,4 tony przyprawy na godzinę.
Ile saszetek maszyna zapakuje w ciągu 8 minut?
A) 1600 saszetek B) 200 saszetek C) 2400 saszetek D) 1200 saszetek
Do udziału w podchodach zgłosiło się 54 chłopców i 24 dziewczynki. Uczestników postanowiono podzielić na zespoły w ten sposób, aby we wszystkich zespołach była ta sama liczba dziewcząt i ta sama liczba chłopców.
Ile maksymalnie zespołów utworzono?
A) 9 B) 2 C) 3 D) 6
Z trójkąta 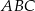 o obwodzie 50 wycięto kwadrat
o obwodzie 50 wycięto kwadrat 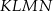 o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
A) 64 B) 60 C) 75 D) 70
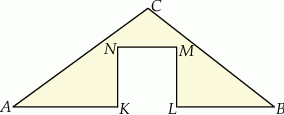
W sześciokąt foremny 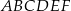 wpisano trójkąt równoboczny tak jak przedstawiono na rysunku.
wpisano trójkąt równoboczny tak jak przedstawiono na rysunku.
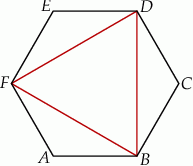
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód trójkąta 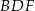 jest większy niż 80% obwodu sześciokąta jest większy niż 80% obwodu sześciokąta 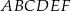 . . | P | F |
Pole trójkąta 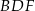 jest 3 razy większe od pola trójkąta jest 3 razy większe od pola trójkąta 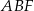 . . | P | F |
Równanie 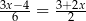
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Równanie 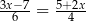
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Równanie 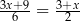
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Automat biletowy drukuje 30 biletów w ciągu 2 minut i 6 sekund. Który wzór opisuje zależność między liczbą wydrukowanych biletów ( ), a czasem ich druku w sekundach (
), a czasem ich druku w sekundach (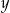 ), jeżeli tempo drukowania biletów nie ulega zmianie?
), jeżeli tempo drukowania biletów nie ulega zmianie?
A) 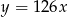 B)
B) 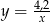 C)
C) 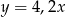 D)
D) 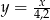
Jeżeli odcinek 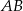 podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części (
podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części ( ), na którą dzielimy odcinek
), na którą dzielimy odcinek 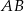 , a długością (
, a długością (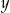 ) jednej takiej części w milimetrach?
) jednej takiej części w milimetrach?
A) 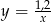 B)
B) 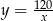 C)
C) 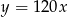 D)
D) 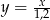
Na rysunku poniżej przedstawiono siatkę pewnej bryły. Punkty: 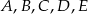 są środkami jej krawędzi.
są środkami jej krawędzi.
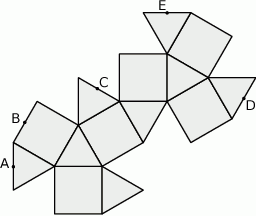
Po złożeniu bryły z tej siatki punkt 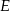 pokryje się z punktem
pokryje się z punktem
A) 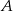 B)
B) 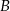 C)
C) 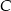 D)
D) 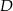
Wyrażenie 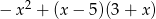 można przekształcić do postaci
można przekształcić do postaci
A) 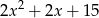 B)
B) 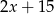 C)
C) 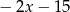 D)
D) 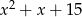
Wyrażenie 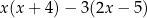 można przekształcić równoważnie do postaci
można przekształcić równoważnie do postaci
A) 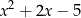 B)
B) 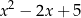 C)
C) 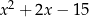 D)
D) 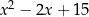
Wyrażenie 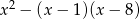 można przekształcić do postaci
można przekształcić do postaci
A) 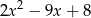 B)
B) 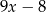 C)
C) 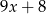 D)
D) 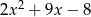
Wyrażenie 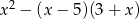 można przekształcić do postaci
można przekształcić do postaci
A) 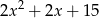 B)
B) 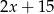 C)
C) 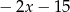 D)
D) 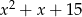
W trapezie prostokątnym kąt ostry ma miarę 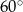 , a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
, a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
A) 6 B) 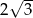 C)
C) 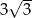 D)
D) 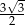
W trapezie prostokątnym kąt ostry ma miarę 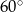 , a podstawy mają długości 10 i 8. Wysokość tego trapezu jest równa
, a podstawy mają długości 10 i 8. Wysokość tego trapezu jest równa
A) 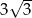 B) 4 C)
B) 4 C) 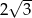 D)
D) 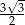
W trapezie prostokątnym kąt ostry ma miarę 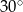 , a podstawy mają długości 8 i 10. Wysokość tego trapezu jest równa
, a podstawy mają długości 8 i 10. Wysokość tego trapezu jest równa
A) 4 B) 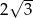 C)
C) 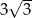 D)
D) 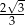
W trapezie prostokątnym kąt ostry ma miarę 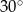 , a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
, a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
A) 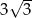 B)
B) 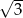 C) 6 D)
C) 6 D)