Zadanie nr 6339978
Wykaż, że środki boków rombu są wierzchołkami prostokąta.
Rozwiązanie
Rozpoczynamy od rysunku.
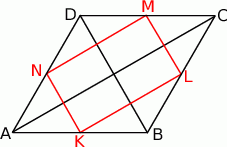
Zauważmy, że odcinki 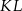 i
i  łączą środki boków odpowiednio w trójkątach
łączą środki boków odpowiednio w trójkątach  i
i 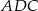 . Są więc one równoległe do przekątnej
. Są więc one równoległe do przekątnej 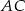 . Podobnie uzasadniamy, że odcinki
. Podobnie uzasadniamy, że odcinki 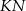 i
i 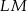 są równoległe do przekątnej
są równoległe do przekątnej 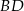 . W takim razie czworokąt
. W takim razie czworokąt 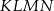 jest równoległobokiem. Co więcej, przekątne rombu są prostopadłe, więc odcinki
jest równoległobokiem. Co więcej, przekątne rombu są prostopadłe, więc odcinki 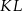 i
i 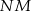 są prostopadłe do odcinków
są prostopadłe do odcinków 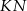 i
i 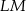 , co dowodzi, że czworokąt
, co dowodzi, że czworokąt 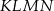 jest prostokątem.
jest prostokątem.

