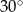Zadanie nr 7454933
- Uzasadnij, że
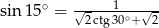
- W równoległoboku
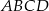 dane są miary kątów
dane są miary kątów 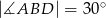 i
i 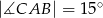 . Oblicz miarę kąta
. Oblicz miarę kąta 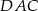 .
.
Rozwiązanie
- Wiemy, że
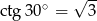 , spróbujmy jeszcze wyliczyć
, spróbujmy jeszcze wyliczyć 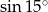 . Korzystamy ze wzoru
. Korzystamy ze wzoru 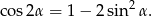
Mamy zatem
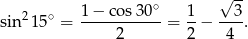
Aby wykazać żądaną równość liczymy kwadrat jej prawej strony.
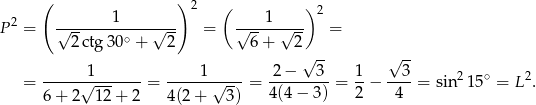
Obie strony są dodatnie, więc możemy opuścić kwadraty.
-
Sposób I
Zaczynamy od rysunku.
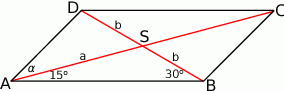
Zauważmy, że
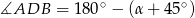 . Napiszmy teraz twierdzenia sinusów w trójkątach
. Napiszmy teraz twierdzenia sinusów w trójkątach  i
i  (poprzedni podpunkt trochę nam podpowiada jak to zrobić).
(poprzedni podpunkt trochę nam podpowiada jak to zrobić). 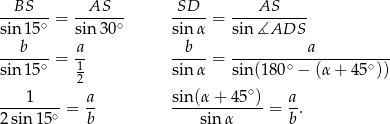
Porównując te dwie równości i korzystając z pierwszego punktu mamy
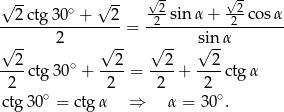
Sposób II
Zadanie można też rozwiązać nie używając trygonometrii, choć wymaga to odrobiny spostrzegawczości.
Dorysujmy wysokość
 równoległoboku i połączmy punkt
równoległoboku i połączmy punkt  z punktem
z punktem 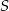 . Zauważmy, że odcinek
. Zauważmy, że odcinek 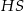 jest środkową w trójkącie prostokątnym
jest środkową w trójkącie prostokątnym 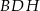 . To oznacza, że
. To oznacza, że 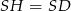 , bo
, bo 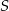 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 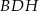 i oba odcinki mają długość równą promieniowi tego okręgu. W takim razie trójkąt
i oba odcinki mają długość równą promieniowi tego okręgu. W takim razie trójkąt 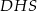 jest równoboczny (bo jest równoramienny i ma kąt
jest równoboczny (bo jest równoramienny i ma kąt 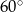 ). W takim razie
). W takim razie 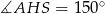 oraz
oraz 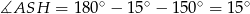
co oznacza, że trójkąt
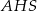 jest równoramienny. W szczególności
jest równoramienny. W szczególności 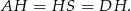
To z kolei oznacza, że trójkąt
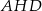 jest równoramienny i prostokątny, czyli
jest równoramienny i prostokątny, czyli 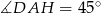 . Stąd
. Stąd 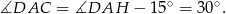
Odpowiedź: