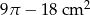/Szkoła średnia/Geometria/Planimetria/Czworokąt/Kwadrat/Pole

Zadanie nr 4070779

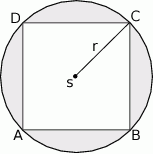
Na kwadracie 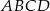ABCD opisano okrąg o promieniu 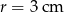r = 3 cm . Oblicz pole zacieniowanej ﬁgury.

Całe pole koła jest równe

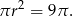
2 πr = 9π.

Obliczmy długość boku kwadratu

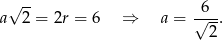
√ -- 6 a 2 = 2r = 6 ⇒ a = √---. 2

W takim razie pole kwadratu jest równe

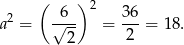
( ) 2 a2 = √6-- = 36-= 18. 2 2

Pole zacieniowanej ﬁgury jest więc równe

9π − 18 .

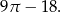
Odpowiedź: 9π − 18 cm 2