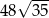Zadanie nr 9435485
Suma długości wszystkich krawędzi ostrosłupa prawidłowego trójkątnego jest równa 96, a krawędź boczna tworzy z płaszczyzną podstawy kąt, którego cosinus jest równy 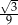 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Rozwiązanie
Szkicujemy opisaną sytuację.
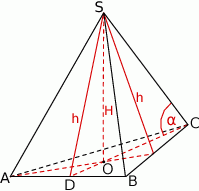
Oznaczmy przez  długość krawędzi podstawy. Spodek wysokości
długość krawędzi podstawy. Spodek wysokości  ostrosłupa dzieli wysokości trójkąta równobocznego w podstawie w stosunku 2:1, więc
ostrosłupa dzieli wysokości trójkąta równobocznego w podstawie w stosunku 2:1, więc
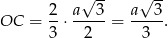
Korzystamy teraz z podanego cosinusa kąta nachylenia krawędzi bocznej do płaszczyzny podstawy.
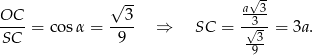
Korzystamy teraz z podanej sumy długości wszystkich krawędzi ostrosłupa.
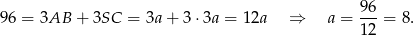
Obliczamy teraz wysokość 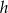 ściany bocznej
ściany bocznej
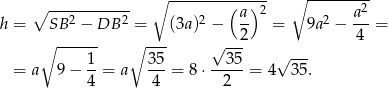
Obliczamy pole powierzchni bocznej.
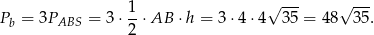
Odpowiedź: