Zadanie nr 7282110
Dany jest ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość  i krawędź boczna jest od niej dwa razy dłuższa. Oblicz cosinus kąta między krawędzią boczną i krawędzią podstawy ostrosłupa. Narysuj przekrój ostrosłupa płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej krawędzi bocznej i oblicz pole tego przekroju.
i krawędź boczna jest od niej dwa razy dłuższa. Oblicz cosinus kąta między krawędzią boczną i krawędzią podstawy ostrosłupa. Narysuj przekrój ostrosłupa płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej krawędzi bocznej i oblicz pole tego przekroju.
Rozwiązanie
Zaczynamy oczywiście od rysunku.
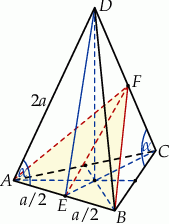
Żądany cosinus łatwo obliczyć z trójkąta prostokątnego 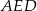 :
:
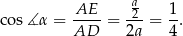
Aby obliczyć pole przekroju potrzebujemy wyliczyć długość wysokości 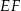 trójkąta równoramiennego
trójkąta równoramiennego 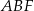 . Obliczony cosinus podpowiada nam jak to zrobić: stosujemy najpierw twierdzenie cosinusów w trójkącie
. Obliczony cosinus podpowiada nam jak to zrobić: stosujemy najpierw twierdzenie cosinusów w trójkącie 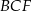
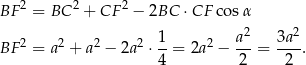
Teraz stosujemy twierdzenie Pitagorasa w trójkącie 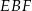 .
.
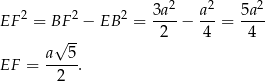
Zatem szukane pole przekroju jest równe
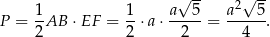
Odpowiedź: Cosinus: 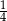 , pole:
, pole: 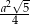 .
.

