/Szkoła średnia/Liczby/Liczby całkowite/Podzielność/1 literka

Zadanie nr 6229239

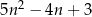Wykaż, że dla każdej liczby całkowitej nieparzystej liczba 2 5n − 4n + 3 jest podzielna przez 4.

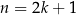Jeżeli jest liczbą nieparzystą, to możemy ją zapisać w postaci n = 2k+ 1 , dla pewnej liczby całkowitej 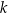. Mamy wtedy

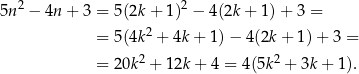
5n 2 − 4n + 3 = 5(2k + 1)2 − 4(2k + 1) + 3 = 2 = 5(4k + 4k + 1) − 4(2k + 1) + 3 = = 20k2 + 12k + 4 = 4(5k2 + 3k+ 1).

Oczywiście liczba ta dzieli się przez 4.