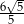/Szkoła średnia/Geometria/Geometria analityczna/Przekształcenia/Symetria środkowa

Zadanie nr 3139479

Dodaj do ulubionych
Dodaj do rozwiązanych

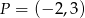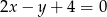Dany jest punkt P = (− 2,3) i prosta k o równaniu 2x − y + 4 = 0 .

  • Wyznacz równanie prostej 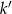k′ , która jest obrazem prostej 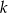k w symetrii względem punktu P .
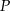  • Oblicz odległość między prostymi 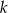k i ′ k .

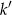Rozwiązanie

PIC

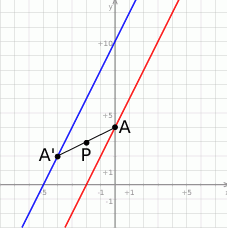
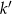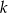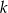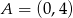  • Jak to zwykle w zadaniach z geometrii analitycznej istnieje wiele możliwych rozwiązań. My zrobimy to nastepująco: ponieważ znamy współczynnik kierunkowy prostej ′ k (bo jest taki sam jak prostej k ), to aby napisać równanie tej prostej potrzebujemy znaleźć jeden jej punkt. Chyba najprostszy na to sposób, to wziąć jakikolwiek punkt prostej k , np. 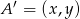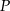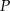A = (0,4) i skorzystać z faktu, że jeżeli punkt A ′ = (x ,y) jest obrazem tego punktu w symetrii względem punktu P , to P jest środkiem odcinka 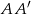′ AA (inny sposób to skorzystanie z równości: 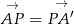→ A→P = PA ′ ). Mamy zatem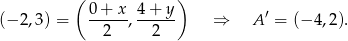
    ( 0+ x 4+ y ) (− 2,3) = -----, ------ ⇒ A ′ = (− 4,2). 2 2

    Jak już zauważyliśmy, szukana prosta jest postaci 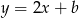y = 2x+ b . Pozostało wyznaczyć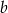 b

    2 = −8 + b ⇒ b = 10.

     
    Odpowiedź: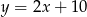 y = 2x + 10

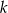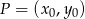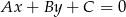  • Szukana odległość jest dwa razy większa niż odległość punktu P od prostej k . Korzystamy ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :
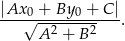
    |Ax + By + C | ---√0-----0------. A 2 + B2

    W naszej sytuacji mamy

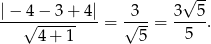
    √ -- |−-√4−--3+--4|= √3--= 3--5-. 4 + 1 5 5

     
    Odpowiedź: 6√5- 5

Wersja PDF
Rozwiązanie Losuj ponownie