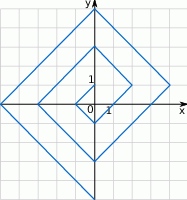
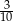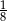Punkt kratowy to miejsce przecięcia się linii kwadratowej siatki. Pole wielokąta, którego wierzchołki znajdują się w punktach kratowych kwadratowej siatki na płaszczyźnie, można obliczyć ze wzoru Picka:
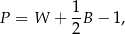
gdzie 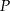 oznacza pole wielokąta,
oznacza pole wielokąta, 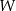 – liczbę punktów kratowych leżących wewnątrz wielokąta, a
– liczbę punktów kratowych leżących wewnątrz wielokąta, a 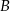 – liczbę punktów kratowych leżących na brzegu tego wielokąta.
– liczbę punktów kratowych leżących na brzegu tego wielokąta.
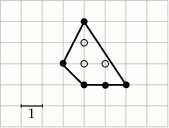
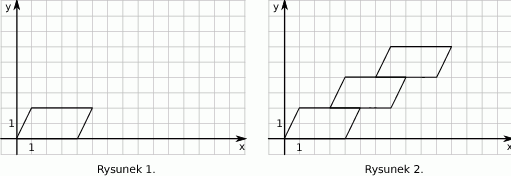
W wielokącie przedstawionym na rysunku 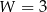 oraz
oraz 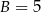 , zatem
, zatem 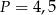 .
.
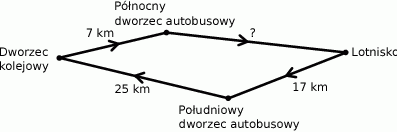
Wewnątrz pewnego wielokąta znajduje się 5 punktów kratowych, a na jego brzegu jest 6 punktów kratowych. Pole tego wielokąta jest równe
A) 6 B) 6,5 C) 7 D) 7,5

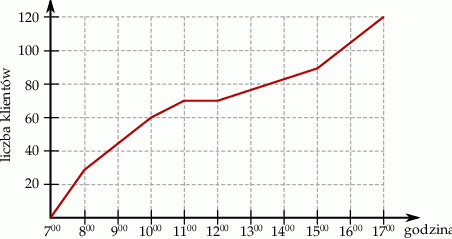
 do
do 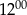 do sklepu nie przyszedł żaden klient.
do sklepu nie przyszedł żaden klient. 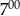 do
do 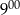 sklep odwiedziło mniej klientów niż od
sklep odwiedziło mniej klientów niż od 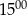 do
do  .
. 
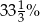
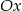 , przesunięcia o 3 jednostki w prawo, i odsunięcia o 1 jednostkę od osi
, przesunięcia o 3 jednostki w prawo, i odsunięcia o 1 jednostkę od osi  (rysunek 2.).
(rysunek 2.). 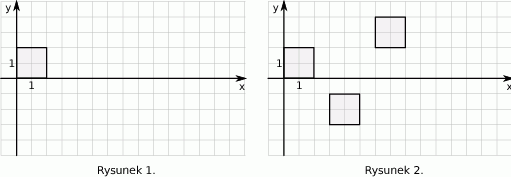
 środka tego kwadratu jest równa
środka tego kwadratu jest równa 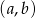 i
i 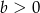 , to współrzędne środka kolejnego kwadratu będą równe
, to współrzędne środka kolejnego kwadratu będą równe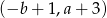
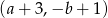
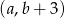
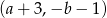
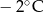
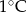
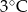
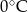
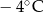
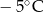
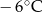
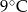
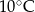
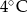
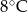
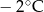 .
.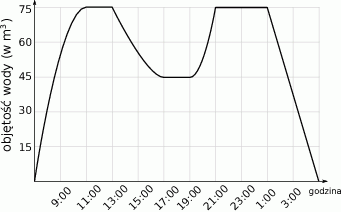
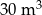
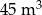
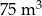
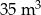
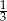 objętości wody usunięto w ciągu
objętości wody usunięto w ciągu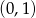 budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość
budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość 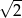 .
. 
 jest liczbą parzystą, to odcinek o numerze
jest liczbą parzystą, to odcinek o numerze  jest równoległydo odcinka o numerze 3.
jest równoległydo odcinka o numerze 3. jest liczbą nieparzystą, to długość odcinka o numerze
jest liczbą nieparzystą, to długość odcinka o numerze  jest równa
jest równa 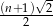 .
. 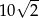 .
.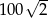 .
. 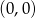 budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2.
budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2. 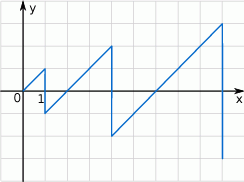
 jest liczbą nieparzystą, to odcinek o numerze
jest liczbą nieparzystą, to odcinek o numerze  jest równoległy doodcinka o numerze 1.
jest równoległy doodcinka o numerze 1. jest liczbą parzystą, to długość odcinka o numerze
jest liczbą parzystą, to długość odcinka o numerze  jest równa
jest równa 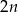 .
. 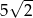 .
.  jest liczbą parzystą, to długość odcinka o numerze
jest liczbą parzystą, to długość odcinka o numerze 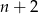 jest o 2 większa od długości odcinka o numerze
jest o 2 większa od długości odcinka o numerze  .
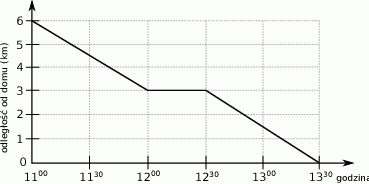
.  do miasta
do miasta  w zależności od czasu jazdy.
w zależności od czasu jazdy. 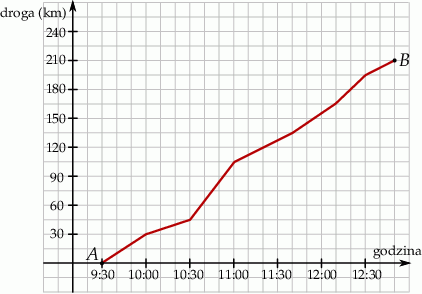
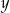 prawego górnego wierzchołka tego równoległoboku jest równa
prawego górnego wierzchołka tego równoległoboku jest równa . Współrzędne takiego wierzchołka w następnym równoległoboku będą równe
. Współrzędne takiego wierzchołka w następnym równoległoboku będą równe
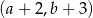
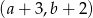
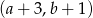
 równoległoboków. Współrzędna y prawego górnego wierzchołka ostatniego równoległoboku jest równa
równoległoboków. Współrzędna y prawego górnego wierzchołka ostatniego równoległoboku jest równa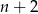
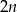
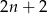
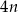
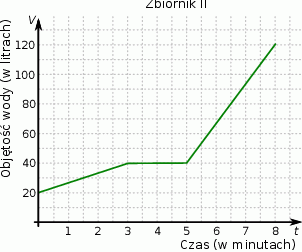
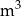 ) od czasu pracy pomp (w godzinach).
) od czasu pracy pomp (w godzinach). 
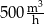
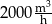
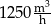
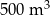 wody.
wody. 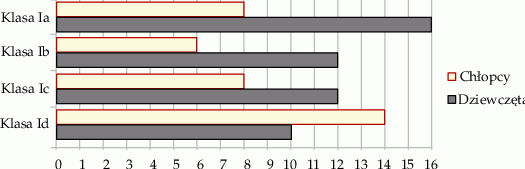
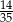
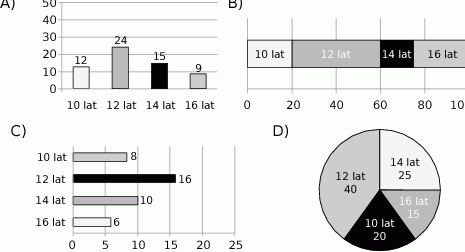
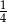 , to w pierwszym losowaniu nie wyciągnięto żadnej piłki czerwonej.
, to w pierwszym losowaniu nie wyciągnięto żadnej piłki czerwonej.