Aby dobrać rozmiar ramy roweru do wzrostu użytkownika, można posłużyć się następującą regułą: rozmiar odpowiedniej ramy otrzymamy, gdy od 40% wzrostu użytkownika (w cm) odejmiemy 15 cm.
Jaki rozmiar powinna mieć, według tej reguły, rama dla rowerzysty o wzroście 175 cm?
A) 55 cm B) 64 cm C) 90 cm D) 96 cm
/Szkoła podstawowa/Zadania testowe/Bloki zadań
Niech  oznacza rozmiar ramy (w cm),
oznacza rozmiar ramy (w cm), 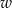 – wzrost użytkownika (też w cm).
– wzrost użytkownika (też w cm).
Którym wzorem nie można wyrazić opisanej wyżej reguły dobierania rozmiaru ramy?
A) 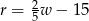 B)
B) 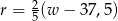 C)
C) 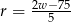 D)
D) 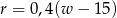
Wykres przedstawia liczbę pasażerów w autobusie w trakcie kolejnych kursów.
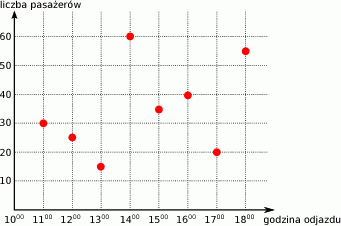
Ilu pasażerów jechało autobusem o godzinie 14:00?
A) 20 B) 40 C) 50 D) 60
O ilu więcej pasażerów jechało o 16:00 niż o 12:00?
A) o 5 B) o 20 C) o 10 D) o 15
O której godzinie w autobusie było 15 pasażerów?
A) o 13:00 B) o 14:00 C) o 17:00 D) o żadnej
Ile razy więcej pasażerów jechało autobusem o 16:00, niż o 17:00?
A) 20 razy B) 2 razy C) 1,5 raza D) nie można tego obliczyć
Trójki liczb naturalnych 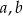 i
i  , które spełniają warunek
, które spełniają warunek 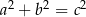 , nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
, nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
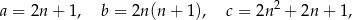
gdzie  oznacza dowolną liczbę naturalną (
oznacza dowolną liczbę naturalną (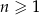 ).
).
Liczba  zawsze będzie A/B.
zawsze będzie A/B.
A) parzysta B) nieparzysta
Liczby 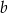 i
i  różnią się o C/D.
różnią się o C/D.
C) 1 D) 
Liczba 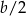 zawsze będzie A/B.
zawsze będzie A/B.
A) parzysta B) nieparzysta
Liczby 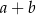 i
i  różnią się o C/D.
różnią się o C/D.
C) 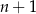 D)
D) 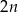
Jeżeli najmniejsza z liczb 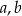 i
i  jest równa 9, to największa z tych liczb jest równa
jest równa 9, to największa z tych liczb jest równa
A) 41 B) 73 C) 145 D) 181
Jeżeli najmniejsza z liczb 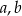 i
i  jest równa 11, to największa z tych liczb jest równa
jest równa 11, to największa z tych liczb jest równa
A) 265 B) 73 C) 145 D) 61
W tabeli przedstawiono informacje dotyczące wyników sprawdzianu z matematyki.
| Ocena | Liczba uczniów |
| 2 | 3 |
| 3 | 8 |
| 4 | 5 |
| 5 | 4 |
A) 2 B) 2,5 C) 3 D) 3,5
Na którym diagramie poprawnie przedstawiono procentowy podział uczniów ze względu na uzyskaną ocenę?
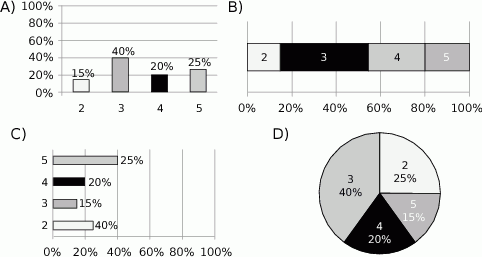
W tabeli przedstawiono informacje dotyczące wieku wszystkich uczestników obozu narciarskiego.
| Wiek uczestnika | Liczba uczestników |
| 10 lat | 5 |
| 14 lat | 3 |
| 15 lat | 4 |
| 16 lat | 8 |
A) 14 lat B) 14,5 roku C) 15 lat D) 15,5 roku
Na którym diagramie poprawnie przedstawiono procentowy podział uczestników obozu ze względu na wiek?
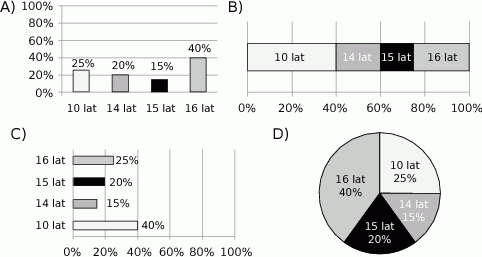
Promocja w zakładzie optycznym jest związana z wiekiem klienta i polega na tym, że klient otrzymuje tyle procent zniżki, ile ma lat.
Cena okularów bez promocji wynosi 240 zł. Ile zapłaci za te okulary klient, który ma 35 lat?
A) 84 zł B) 132 zł C) 156 zł D) 205 zł
Okulary bez promocji kosztują 450 zł, a klient zgodnie z obowiązującą promocją może je kupić za 288 zł. Ile lat ma ten klient?
A) 64 B) 56 C) 44 D) 36
Jeżeli 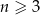 , to liczbę przekątnych wielokąta wypukłego o
, to liczbę przekątnych wielokąta wypukłego o  bokach można obliczyć ze wzoru
bokach można obliczyć ze wzoru
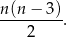
Wielokąt, który ma cztery razy więcej przekątnych niż boków ma A/B boków.
A) 10 B) 11
Liczba przekątnych wielokąta o 222 bokach jest liczbą C/D.
C) nieparzystą D) parzystą
Która z liczb nie jest liczbą przekątnych pewnego wielokąta wypukłego?
A) 5 B) 9 C) 10 D) 14 E) 20
Poniżej opisano kilka zależności.
1) Im większy bok kwadratu, tym większe jego pole.
2) Im większy bok kwadratu, tym większy jego obwód.
3) Im większa cena 1 kg ziemniaków, tym więcej zapłacimy za 2 kg.
4) Im większa cena 1 kg ziemniaków, tym mniej kupimy za 4 zł.
5) Im więcej wydaliśmy z 10 zł, tym mniej nam zostało.
Które z przedstawionych zależności są proporcjonalnością prostą?
A) 1, 2 i 3 B) tylko 2 i 3 C) tylko 1 i 2 D) tylko 3 i 4
Która z przedstawionych powyżej zależności jest opisana danym wykresem
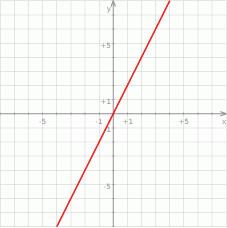
A) 5 B) 4 C) 3 D) 2
Która z przedstawionych powyżej zależności jest opisana danym wykresem
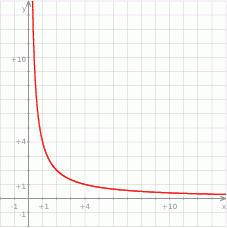
A) 4 B) 3 C) 2 D) 1
Które z przedstawionych zależności są proporcjonalnością odwrotną?
A) 4, 5,6 B) tylko 4 C) tylko 5 D) 3, 4, 5
Mateusz mieszka w odległości 4 km od szkoły. Część drogi do szkoły pokonuje pieszo, idąc do przystanku autobusowego. Tam czeka na autobus, a następnie wsiada do niego i jedzie do szkoły. Pewnego dnia, gdy był już na przystanku, stwierdził, że zapomniał zabrać zeszyt, więc wrócił po niego do domu. Wykres przedstawia, jak tego dnia zmieniała się odległość Mateusza od domu w zależności od czasu.
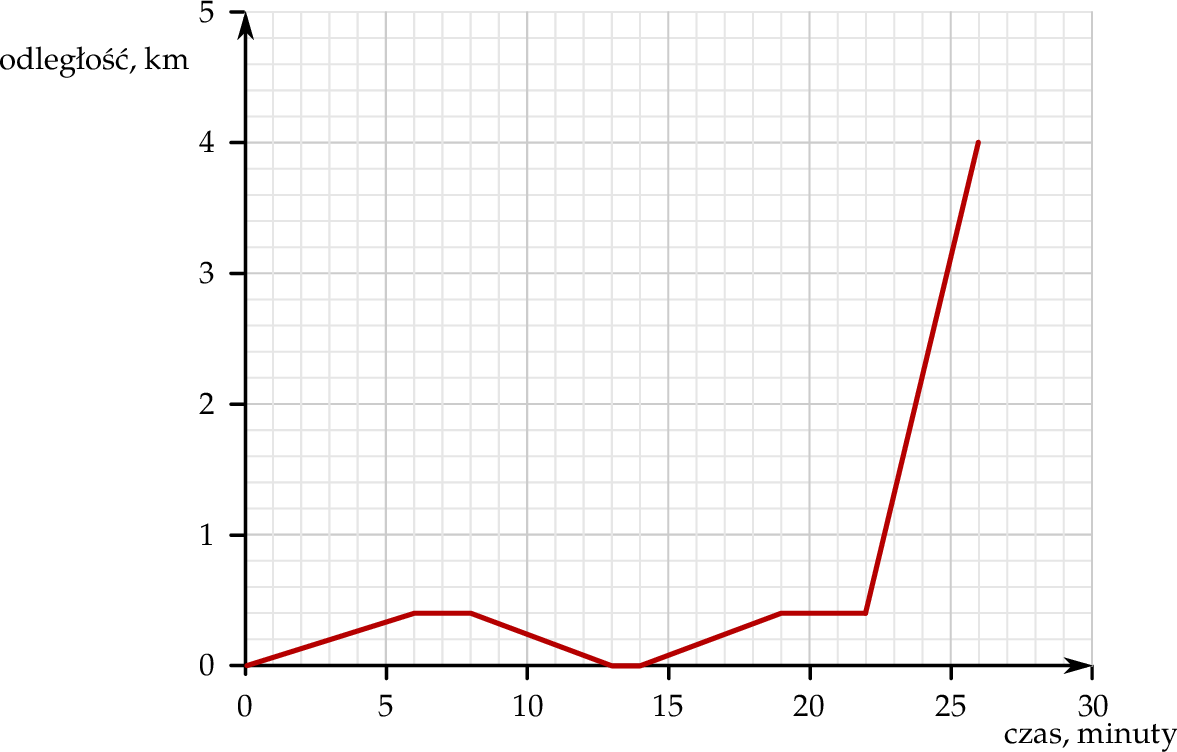
Od momentu, gdy Mateusz zawrócił z przystanku do domu, do momentu, gdy dotarł ponownie na przystanek, upłynęło
A) 11 minut. B) 13 minut. C) 14 minut. D) 16 minut.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dom Mateusza znajduje się w odległości 400 m od przystanku autobusowego. | P | F |
Autobus drogę między przystankami pokonał z prędkością 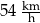 . . | P | F |
Jeżeli 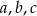 i
i 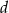 są długościami kolejnych boków czworokąta, to przekątne tego czworokąta są prostopadłe wtedy i tylko wtedy, gdy
są długościami kolejnych boków czworokąta, to przekątne tego czworokąta są prostopadłe wtedy i tylko wtedy, gdy 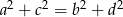 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Czworokąt, którego dwa przeciwległe boki mają długości 7 i 24, a dwa pozostałe boki mają długości 15 i 20 ma prostopadłe przekątne. | P | F |
Czworokąt, w którym długości kolejnych boków są równe: 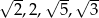 ma prostopadłe przekątne. ma prostopadłe przekątne. | P | F |
Jeżeli trzy kolejne boki czworokąta mają długości: 5, 6, 7 oraz przekątne tego czworokąta są prostopadłe, to czwarty bok tego czworokąta ma długość
A) 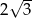 B)
B) 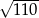 C)
C) 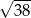 D)
D) 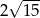
W poniedziałek pan Ryszard, mieszkaniec wsi Janki, odwiózł córkę do szkoły w Gródku, a następnie pojechał na kontrolę swoich sklepów w Sowach i w Migocku. Na schematycznej mapce przedstawiono drogi łączące te miejscowości, a na wykresie – jak zmieniała się w czasie tej podróży odległość (mierzona w linii prostej) pana Ryszarda od domu.
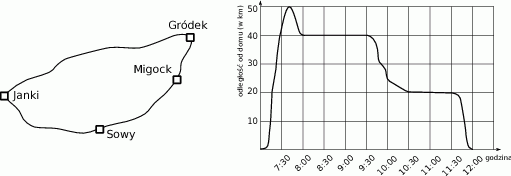
Jaka jest odległość (w linii prostej) między Jankami a Gródkiem?
A) 50 km B) 40 km C) 20 km D) 10 km
Z podanych informacji wynika, że pan Ryszard
A) najpierw kontrolował sklep w Sowach.
B) między Sowami a Migockiem zatrzymał się na 15 minut.
C) wrócił do domu po 4 godzinach.
D) kontrolował sklep w Sowach co najwyżej godzinę.
Na rysunkach przedstawiono kształt i sposób układania płytek oraz niektóre wymiary w centymetrach.
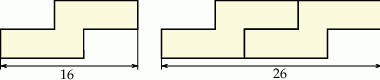
Ułożono wzór z 4 płytek, jak na rysunku.

Odcinek
 ma długość
ma długośćA) 46 cm B) 64 cm C) 36 cm D) 52 cm
Które wyrażenie algebraiczne opisuje długość analogicznego do  odcinka dla wzoru złożonego z
odcinka dla wzoru złożonego z  płytek?
płytek?
A) 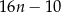 B)
B) 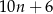 C)
C) 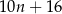 D)
D) 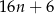
Wykres przedstawia liczbę pasażerów w autobusie w trakcie kolejnych kursów.
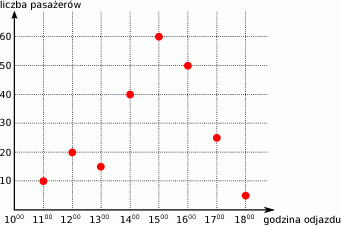
Ilu pasażerów jechało autobusem o godzinie 14:00?
A) 20 B) 40 C) 50 D) 60
Ile razy więcej pasażerów jechało autobusem o 15:00, niż o 14:00?
A) 20 razy B) 2 razy C) 1,5 raza D) nie można tego obliczyć
O ilu więcej pasażerów jechało o 15:00 niż o 12:00?
A) o 5 B) o 30 C) o 40 D) o 60
O której godzinie w autobusie było 25 pasażerów?
A) o 13:00 B) o 14:00 C) o 17:00 D) o żadnej
W sobotę Patrycja wyruszyła z Ptasiej Doliny na górski spacer, w trakcie którego odwiedziła kolejno dwa pobliskie szczyty: Kaczą Górę i Łąbędzią Górę. Na schematycznej mapce przedstawiono drogę jaką pokonała Patrycja, a na wykresie – jak zmieniała się w trakcie spaceru jej względna wysokość (w metrach) mierzona od poziomu Ptasiej Doliny.
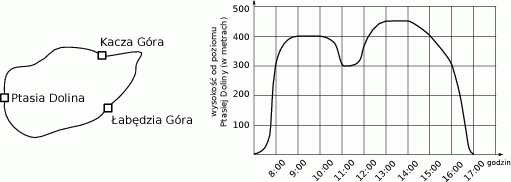
Jaka jest różnica wysokości między Łabędzią Górą, a Kaczą Górą?
A) 50 m B) 100 m C) 150 m D) 400 m
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na każdym ze szczytów Patrycja zrobiła godzinną przerwę. | P | F |
| Od momentu zejścia z Kaczej Góry do momentu wejścia na Łąbędzią Górę upłynęły 4 godziny. | P | F |
| Patrycja wróciła do punktu wyjścia po 9 godzinach. | P | F |
| W ciągu przedostatniej godziny spaceru Patrycja zeszła w dół o 100 metrów. | P | F |
W stadninie koni pani Lucyny znajduje się 120 koni w czterech różnych umaszczeniach. Na diagramie przedstawiono w procentach udział poszczególnych umaszczeń, ale nie narysowano słupka z umaszczeniem karym.
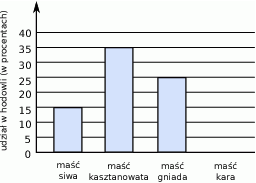
Ile jest koni gniadych w hodowli pani Lucyny?
A) 15 B) 20 C) 25 D) 30
Jaki procent hodowli pani Lucyny stanowią konie kare?
A) 15% B) 20% C) 25% D) 30%
Na rysunkach przedstawiono kształt i sposób układania płytek oraz niektóre wymiary w centymetrach.
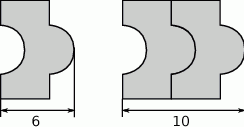
Ułożono wzór z 5 płytek, jak na rysunku.
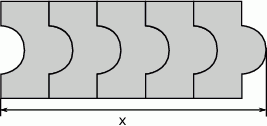
Odcinek
 ma długość
ma długośćA) 20 cm B) 22 cm C) 26 cm D) 30 cm
Które wyrażenie algebraiczne opisuje długość analogicznego do  odcinka dla wzoru złożonego z
odcinka dla wzoru złożonego z  płytek?
płytek?
A) 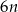 B)
B) 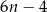 C)
C) 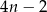 D)
D) 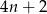
W tabeli podano, w jaki sposób zmienia się cena biletu na 1 przejazd metrem w zależności od pory dnia.
| Cena podstawowa biletu | 8 zł |
| Cena biletu w godzinach 16–18 | cena podstawowa podwyższona o 14% |
| Cena biletu w godzinach 7–8 | cena podstawowa podwyższona o 52% |
| Cena biletu w godzinach 22–24 | cena podstawowa obniżona o 36% |
| Cena biletu w pozostałych godzinach | cena podstawowa |
A) 4 zł B) 7,04 zł C) 1,12 zł D) 4,16 zł
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Cena biletu o godz. 22 jest o 50% niższa niż cena biletu o godz. 17 | P | F |
| Cena biletu o godz. 16 jest o 25% niższa niż cena biletu o godz. 7 | P | F |
Ola przygotowując się do egzaminu rozwiązywała zadania z matematyki. Wykres przedstawia liczbę rozwiązanych zadań w zależności od czasu.
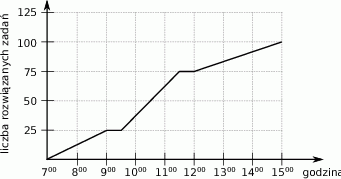
Na podstawie wykresu wybierz zdanie fałszywe.
A) O godzinie
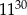 Ola rozpoczęła przerwę.
Ola rozpoczęła przerwę. B) Od
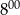 do
do 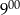 Ola rozwiązała mniej zadań niż od
Ola rozwiązała mniej zadań niż od 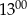 do
do 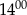 .
. C) Od
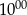 do
do 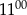 Ola rozwiązywała zadania w tempie 25 zadań na godzinę.
Ola rozwiązywała zadania w tempie 25 zadań na godzinę. D) Przez ostatnie trzy godziny Ola rozwiązała 25 zadań.
Kolejnego dnia Ola ponownie rozwiązywała zadania, ale poświęciła na to 6 godzin. Okazało się jednak, że średnie tempo rozwiązywania zadań było identyczne, jak w dniu przedstawionym na wykresie. Ile zadań Ola rozwiązała drugiego dania nauki?
A) 75 B) 80 C) 90 D) 60
Grupa młodzieży wybrała się na spacer po lesie. W trakcie wycieczki dwukrotnie zrobiono przerwę na odpoczynek. Wykres przedstawia zależność przebytej drogi od czasu trwania spaceru.
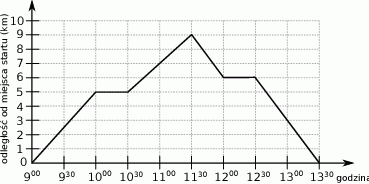
Które z poniższych zdań jest fałszywe?
A) Czas poświęcony na przerwy stanowił ponad 20% czasu całej wycieczki.
B) W trakcie wycieczki młodzież pokonała dystans 9 kilometrów.
C) W ciągu ostatniej godziny młodzież pokonała 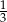 całej trasy.
całej trasy.
D) Pomiędzy przerwami młodzież pokonała dystans 7 kilometrów.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Bezpośrednio przed drugą przerwą prędkość poruszania się grupy była taka sama jak tuż przed zakończeniem wycieczki. | P | F |
| W czasie pomiędzy przerwami grupa poruszała się ze stałą prędkością. | P | F |
W ośrodku szkoleniowym są jednakowe stoliki, których blaty mają kształt trapezów równoramiennych, jak przedstawiono na rysunku 1.

Stoliki można ze sobą łączyć na różne sposoby. Na rysunkach przedstawiono trzy przykładowe zestawienia stolików w stoły konferencyjne oraz sposoby ustawienia przy nich krzeseł.
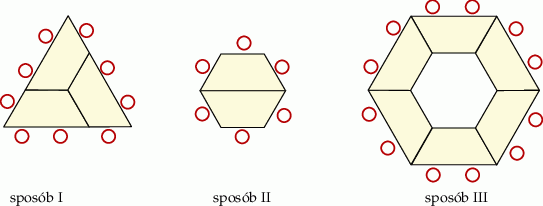
W ośrodku jest 36 stolików. Postanowiono je ustawić w jeden z trzech sposobów pokazanych na powyższych rysunkach. Które z poniższych zdań jest fałszywe?
A) Po ustawieniu wszystkich stolików w sposób I uzyska się tyle samo miejsc siedzących, ile powstaje po ustawieniu wszystkich stolików w sposób II.
B) Najmniejszą liczbę miejsc siedzących uzyska się po ustawieniu wszystkich stolików w sposób III.
C) Po ustawieniu wszystkich stolików w sposób I uzyska się 108 miejsc siedzących.
D) Po ustawieniu wszystkich stolików w sposób II uzyska się 96 miejsc siedzących.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąty trapezu przedstawionego na rysunku 1 mają miary: 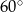 , , 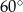 , , 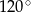 , , 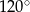 . . | P | F |
| Krótsza podstawa tego trapezu jest 2 razy krótsza od jego dłuższej podstawy. | P | F |

