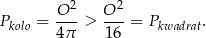Zadanie nr 1814426
Koło i kwadrat mają równe obwody. Wykaż, że pierwsza z tych figur ma większe pole.
Rozwiązanie
Oznaczmy przez 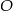 obwód kwadratu i koła, a przez
obwód kwadratu i koła, a przez  bok kwadratu i przez
bok kwadratu i przez  promień koła. Wówczas ze wzorów na obwody otrzymujemy
promień koła. Wówczas ze wzorów na obwody otrzymujemy
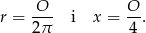
Stąd
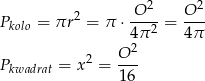
Ponieważ 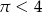 mamy więc
mamy więc