Zadanie nr 2922081
Wykaż, że jeżeli punkt 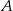 leży na prostej
leży na prostej 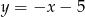 , a punkt
, a punkt 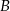 ma współrzędne
ma współrzędne
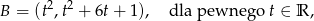
to długość odcinka 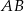 jest nie mniejsza niż
jest nie mniejsza niż 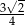 .
.
Rozwiązanie
Trudno wykonać nawet szkicowy rysunek, bo nie wiadomo jak są położone punkty 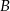 , a więc od razu bierzemy się za rachunki.
, a więc od razu bierzemy się za rachunki.
Jeżeli 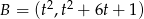 to długość odcinka
to długość odcinka 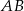 nie może być krótsza niż odległość punktu
nie może być krótsza niż odległość punktu 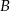 od podanej prostej
od podanej prostej 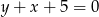 , a odległość ta jest równa
, a odległość ta jest równa
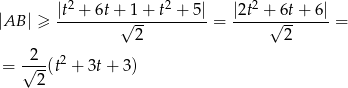
(mogliśmy opuścić wartość bezwzględną, bo znajdujący się pod nią trójmian jest zawsze dodatni).
Sposób I
Musimy wykazać nierówność
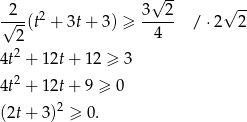
Ponieważ przekształcenia były równoważnościami, wyjściowa nierówność również musiała być prawdziwa.
Sposób II
Wykresem funkcji
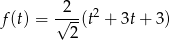
jest parabola o ramionach skierowanych w górę, więc przyjmuje ono najmniejszą wartość w wierzchołku, czyli dla 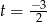 . Wartość ta jest równa
. Wartość ta jest równa
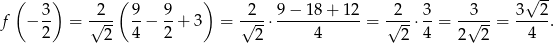
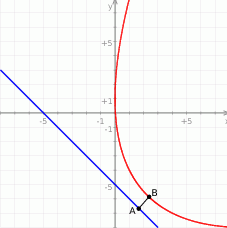
Na koniec obrazek ilustrujący jak naprawdę wygląda cała sytuacja.