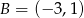Zadanie nr 7579442
W układzie współrzędnych dany jest punkt 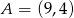 . Na okręgu o równaniu
. Na okręgu o równaniu 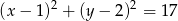 wyznacz współrzędne punktu
wyznacz współrzędne punktu 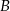 , dla którego odległość
, dla którego odległość 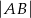 jest największa.
jest największa.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
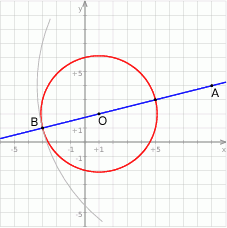
Powinno być jasne, że punkt 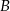 , dla którego odległość
, dla którego odległość 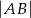 jest największa to jeden z końców średnicy okręgu wyznaczonej przez prostą
jest największa to jeden z końców średnicy okręgu wyznaczonej przez prostą 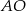 , gdzie
, gdzie 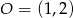 jest środkiem okręgu. Tak jest, bo okrąg o środku
jest środkiem okręgu. Tak jest, bo okrąg o środku 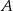 i promieniu
i promieniu 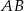 jest styczny do danego okręgu.
jest styczny do danego okręgu.
Sposób I
Zacznijmy od napisania równania prostej 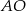 . Do równania postaci
. Do równania postaci 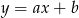 podstawiamy współrzędne punktów
podstawiamy współrzędne punktów 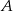 i
i 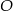 .
.
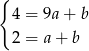
Odejmujemy od pierwszego równania drugie i mamy 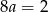 , czyli
, czyli 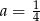 . Zatem
. Zatem
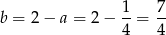
i prosta 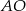 ma równanie
ma równanie 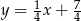 . Szukamy teraz punktów wspólnych tej prostej z danym okręgiem.
. Szukamy teraz punktów wspólnych tej prostej z danym okręgiem.
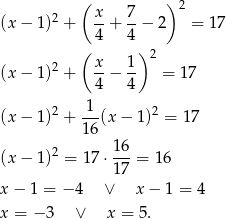
Mamy wtedy odpowiednio 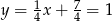 i
i 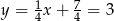 . Zatem
. Zatem 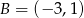 lub
lub 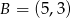 . Patrząc na obrazek (lub licząc odległości
. Patrząc na obrazek (lub licząc odległości 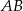 ) stwierdzamy, że interesujący nas punkt to
) stwierdzamy, że interesujący nas punkt to 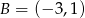 .
.
Sposób II
Zauważmy, że łatwo obliczyć długość odcinka 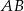 .
.
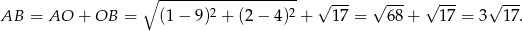
W takim razie punkt 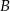 to punkt wspólny danego okręgu o środku
to punkt wspólny danego okręgu o środku 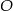 i okręgu o środku
i okręgu o środku 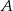 i promieniu
i promieniu 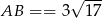 . Musimy więc rozwiązać układ równań
. Musimy więc rozwiązać układ równań
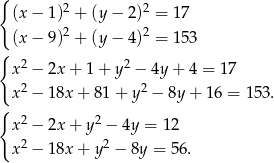
Odejmujemy teraz od pierwszego równania drugie (żeby skrócić kwadraty) i mamy.
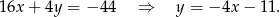
Podstawiamy to wyrażenie do danego równania okręgu.
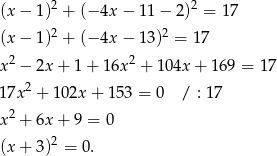
Zatem 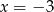 i
i 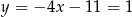 . Stąd
. Stąd 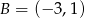 .
.
Odpowiedź: