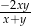Wyrażenie 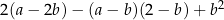 można przekształcić równoważnie do postaci
można przekształcić równoważnie do postaci
A) 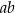 B)
B)  C)
C) 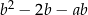 D)
D) 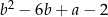 E)
E) 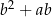
/Szkoła podstawowa/Zadania testowe/Wyrażenia algebraiczne/2 literki
Wyrażenie 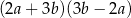 jest równe
jest równe
A) 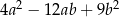 B)
B) 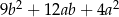 C)
C) 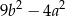 D)
D) 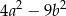
Wyrażenie 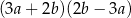 jest równe
jest równe
A) 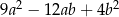 B)
B) 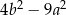 C)
C) 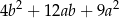 D)
D) 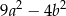
Sprzedawca kupił do swojego sklepu 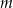 kilogramów marchwi i
kilogramów marchwi i 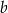 kilogramów buraków: zapłacił po 1,50 zł za kilogram marchwi i po 0,90 zł za kilogram buraków. Warzywa te sprzedał za łączną kwotę 180 złotych. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu?
kilogramów buraków: zapłacił po 1,50 zł za kilogram marchwi i po 0,90 zł za kilogram buraków. Warzywa te sprzedał za łączną kwotę 180 złotych. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu?
A) 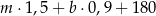 B)
B) 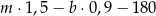
C) 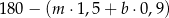 D)
D) 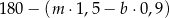
Sprzedawca kupił od ogrodnika róże i tulipany za łączną kwotę 580 zł. Jeden tulipan kosztował 1,20 zł, a cena jednej róży była równa 4 zł. Sprzedawca kupił o 50 tulipanów więcej niż róż. Jeśli liczbę zakupionych tulipanów oznaczymy przez 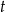 , to podane zależności opisuje równanie
, to podane zależności opisuje równanie
A) 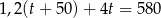 B)
B) 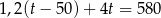
C) 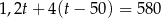 D)
D) 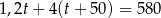
Sprzedawca sprzedał w swoim sklepie 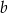 kilogramów bananów i
kilogramów bananów i 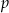 kilogramów pomarańczy: banany sprzedawał po 3,50 zł za kilogram, a pomarańcze po 2,80 zł za kilogram. Na zakup tych warzyw sprzedawca wydał 240 zł. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu?
kilogramów pomarańczy: banany sprzedawał po 3,50 zł za kilogram, a pomarańcze po 2,80 zł za kilogram. Na zakup tych warzyw sprzedawca wydał 240 zł. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu?
A) 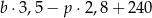 B)
B) 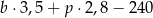
C) 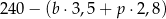 D)
D) 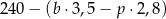
Właściciel sklepu przemysłowego kupił  opakowań 5-kilogramowego proszku do prania w cenie
opakowań 5-kilogramowego proszku do prania w cenie  złotych za kilogram. Zakupiony proszek sprzedał za łączną kwotę 3200 zł. Od uzyskanego przychodu, czyli od różnicy między kwotą uzyskaną ze sprzedaży i kosztami zakupu musi zapłacić podatek dochodowy w wysokości 19%. Które wyrażenie przedstawia wysokość podatku jaki musi zapłacić właściciel tego sklepu?
złotych za kilogram. Zakupiony proszek sprzedał za łączną kwotę 3200 zł. Od uzyskanego przychodu, czyli od różnicy między kwotą uzyskaną ze sprzedaży i kosztami zakupu musi zapłacić podatek dochodowy w wysokości 19%. Które wyrażenie przedstawia wysokość podatku jaki musi zapłacić właściciel tego sklepu?
A) 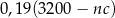 B)
B) 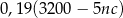
C) 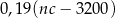 D)
D) 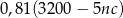
Po skróceniu wyrażenia 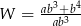 otrzymamy
otrzymamy
A) 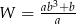 B)
B) 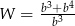 C)
C) 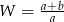 D)
D) 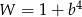
Po skróceniu wyrażenia 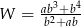 otrzymamy
otrzymamy
A) 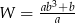 B)
B) 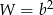 C)
C) 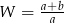 D)
D) 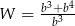
Po skróceniu wyrażenia 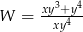 otrzymamy
otrzymamy
A) 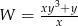 B)
B) 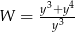 C)
C) 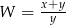 D)
D) 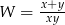
Liczbę  powiększono o 7, a następnie otrzymany wynik zwiększono 4–krotnie. Liczbę
powiększono o 7, a następnie otrzymany wynik zwiększono 4–krotnie. Liczbę 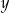 zwiększono 5–krotnie, a otrzymany wynik powiększono o 3. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
zwiększono 5–krotnie, a otrzymany wynik powiększono o 3. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
A) 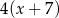 oraz
oraz 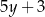 B)
B) 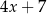 oraz
oraz 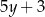
C) 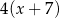 oraz
oraz 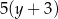 D)
D) 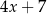 oraz
oraz 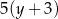
Liczbę  powiększono o 3, a następnie otrzymany wynik zwiększono 7–krotnie. Liczbę
powiększono o 3, a następnie otrzymany wynik zwiększono 7–krotnie. Liczbę 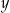 zwiększono 3–krotnie, a otrzymany wynik powiększono o 4. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
zwiększono 3–krotnie, a otrzymany wynik powiększono o 4. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
A) 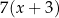 oraz
oraz 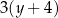 B)
B) 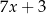 oraz
oraz 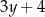
C) 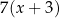 oraz
oraz 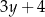 D)
D) 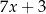 oraz
oraz 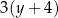
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 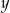 jest dodatnia. Wartość ujemną przyjmuje wyrażenie
jest dodatnia. Wartość ujemną przyjmuje wyrażenie
A) 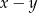 B)
B) 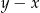 C)
C) 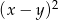 D)
D) 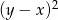
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 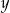 jest dodatnia. Wartość ujemną przyjmuje wyrażenie
jest dodatnia. Wartość ujemną przyjmuje wyrażenie
A) 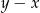 B)
B) 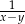 C)
C) 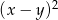 D)
D) 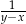
Liczba  jest dodatnia, a liczba
jest dodatnia, a liczba 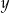 jest ujemna. Wartość ujemną przyjmuje wyrażenie
jest ujemna. Wartość ujemną przyjmuje wyrażenie
A) 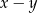 B)
B) 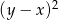 C)
C) 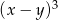 D)
D) 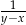
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 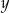 jest dodatnia. Wartość dodatnią przyjmuje wyrażenie
jest dodatnia. Wartość dodatnią przyjmuje wyrażenie
A) 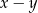 B)
B) 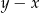 C)
C) 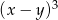 D)
D) 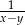
Sześcian wyrażenia 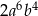 jest równy
jest równy
A) 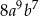 B)
B) 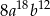 C)
C) 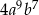 D)
D) 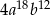
Kwadrat wyrażenia 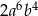 jest równy
jest równy
A) 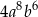 B)
B) 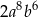 C)
C) 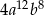 D)
D) 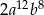
Sześcian wyrażenia 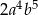 jest równy
jest równy
A) 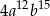 B)
B) 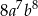 C)
C) 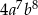 D)
D) 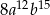
Wyrażenie 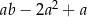 można przekształcić do postaci
można przekształcić do postaci
A) 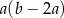 B)
B) 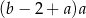 C)
C) 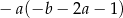 D)
D) 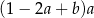
Dane jest wyrażenie 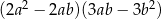 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dane wyrażenie jest równe wyrażeniu 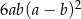 . . | P | F |
Dane wyrażenie jest równe wyrażeniu 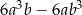 . . | P | F |
Pole wielokąta przedstawionego na rysunku opisuje wyrażenie algebraiczne
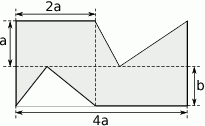
A) 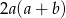 B)
B) 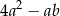 C)
C) 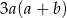 D)
D) 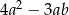
W autobusie jechało 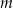 mężczyzn i
mężczyzn i 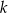 kobiet. Na przystanku wysiedli 2 mężczyźni i 3 kobiety, a wsiadło 5 mężczyzn i 2 kobiety. Gdy autobus odjechał z tego przystanku, podróżowało nim
kobiet. Na przystanku wysiedli 2 mężczyźni i 3 kobiety, a wsiadło 5 mężczyzn i 2 kobiety. Gdy autobus odjechał z tego przystanku, podróżowało nim
A) 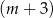 mężczyzn i
mężczyzn i 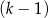 kobiet. B)
kobiet. B) 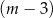 mężczyzn i
mężczyzn i 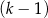 kobiet.
kobiet.
C) 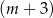 mężczyzn i
mężczyzn i 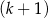 kobiet. D)
kobiet. D) 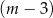 mężczyzn i
mężczyzn i 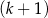 kobiet.
kobiet.
W windzie jechało 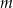 mężczyzn i
mężczyzn i 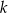 kobiet. Na drugim piętrze wysiadło 3 mężczyzn i 4 kobiety, a wsiadło 2 mężczyzn i 3 kobiety. Gdy winda odjechała z drugiego piętra, znajdowało się w niej
kobiet. Na drugim piętrze wysiadło 3 mężczyzn i 4 kobiety, a wsiadło 2 mężczyzn i 3 kobiety. Gdy winda odjechała z drugiego piętra, znajdowało się w niej
A) 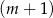 mężczyzn i
mężczyzn i 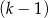 kobiet. B)
kobiet. B) 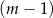 mężczyzn i
mężczyzn i 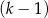 kobiet.
kobiet.
C) 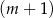 mężczyzn i
mężczyzn i 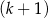 kobiet. D)
kobiet. D) 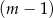 mężczyzn i
mężczyzn i 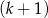 kobiet.
kobiet.
Jeżeli kilogram ziemniaków kosztuje  złotych, a 5 kilogramów ziemniaków kosztuje
złotych, a 5 kilogramów ziemniaków kosztuje 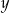 złotych, to
złotych, to
A) 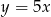 B)
B) 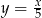 C)
C) 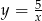 D)
D) 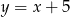
Jeżeli kilogram ziemniaków kosztuje  złotych, a za 5 zł kupiono
złotych, a za 5 zł kupiono 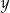 kg ziemniaków, to
kg ziemniaków, to
A) 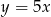 B)
B) 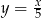 C)
C) 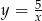 D)
D) 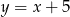
Zdanie: „Liczba  jest o 8 większa od potrojonego kwadratu liczby
jest o 8 większa od potrojonego kwadratu liczby  ” zapisane w postaci równania to
” zapisane w postaci równania to
A) 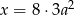 B)
B) 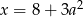 C)
C) 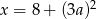 D)
D) 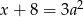
Zdanie: „Liczba  jest 3 razy większa od połowy sześcianu liczby
jest 3 razy większa od połowy sześcianu liczby 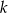 ” zapisane w postaci równania to
” zapisane w postaci równania to
A) 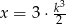 B)
B) 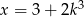 C)
C) 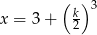 D)
D) 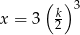
Zdanie: „Liczba  jest o 5 mniejsza od podwojonego kwadratu liczby
jest o 5 mniejsza od podwojonego kwadratu liczby 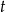 ” zapisane w postaci równania to
” zapisane w postaci równania to
A) 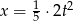 B)
B) 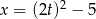 C)
C) 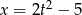 D)
D) 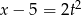
Na rysunku przedstawiono wzór jaki został naniesiony na prostokąt 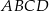 . Wzór ten składa się z 7 prostokątów o bokach
. Wzór ten składa się z 7 prostokątów o bokach  i
i 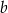 .
.
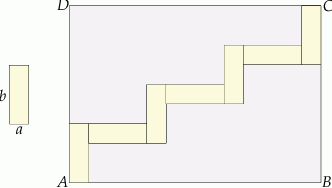
Pole prostokąta 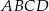 jest równe
jest równe
A) 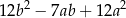 B)
B) 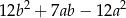 C)
C) 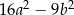 D)
D) 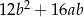
Wyznaczając 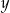 z równania
z równania 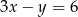 otrzymujemy:
otrzymujemy:
A) 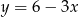 B)
B) 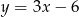 C)
C) 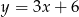 D)
D) 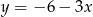
Liczby 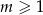 i
i 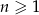 spełniają warunek
spełniają warunek 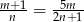 . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 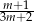 B)
B) 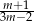 C)
C) 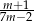 D)
D) 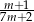
Wiadomo, że liczba 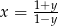 dla
dla 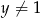 . Zatem
. Zatem
A) 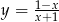 B)
B) 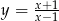 C)
C) 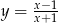 D)
D) 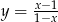
Wiadomo, że liczba 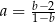 dla
dla 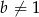 . Zatem
. Zatem
A) 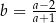 B)
B) 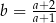 C)
C) 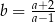 D)
D) 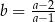
Liczby rzeczywiste  i
i 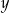 są dodatnie oraz
są dodatnie oraz 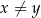 . Wyrażenie
. Wyrażenie 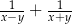 można przekształcić do postaci
można przekształcić do postaci
A) 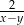 B)
B) 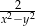 C)
C) 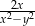 D)
D) 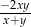
Liczby rzeczywiste  i
i 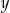 są dodatnie oraz
są dodatnie oraz 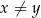 . Wyrażenie
. Wyrażenie 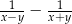 można przekształcić do postaci
można przekształcić do postaci
A) 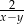 B)
B) 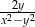 C)
C) 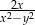 D)
D)