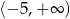/Szkoła średnia/Funkcje/Wielomiany/Przebieg zmienności/Zbiór wartości

Zadanie nr 4068160

Wyznacz zbiór wartości funkcji 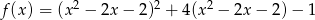2 2 2 f(x) = (x − 2x − 2) + 4 (x − 2x− 2)− 1 .

Rozwiązanie

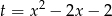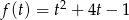Kluczowa w tym zadaniu jest obserwacja, że podana funkcja to złożenie dwóch funkcji kwadratowych. Jeżeli podstawimy t = x2 − 2x − 2 , to f (t) = t2 + 4t− 1 jest zwykłą funkcją kwadratową.

Sposób I

Aby wyznaczyć zbiór wartości tej funkcji musimy najpierw ustalić jak zmienia się 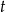. W tym celu musimy wyznaczyć zbiór wartości funkcji 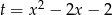t = x2 − 2x − 2 . Wykresem tej funkcji jest parabola o ramionach skierowanych w górę. Druga współrzędna jej wierzchołka (a więc najmniejsza wartość funkcji) to

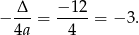
Δ − 12 − --- = -----= − 3. 4a 4

Zatem 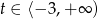t ∈ ⟨− 3,+ ∞ ) . Zbadajmy teraz jakie wartości przyjmuje funkcja 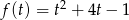2 f (t) = t + 4t− 1 na tym przedziale. Jej wierzchołek ma współrzędne

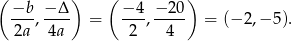
( −b − Δ ) ( − 4 − 20 ) ---,---- = ---,----- = (−2 ,−5 ). 2a 4a 2 4

Ponieważ pierwsza współrzędna wierzchołka znajduje się w przedziale 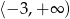⟨− 3,+ ∞ ) , to zbiorem wartości funkcji 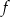jest zbiór 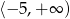⟨− 5,+ ∞ ) – rysunek.

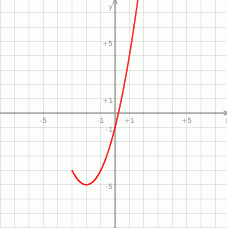
Sposób II

Tym razem zapiszmy funkcję 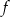w postaci kanonicznej.

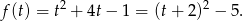
f (t) = t2 + 4t − 1 = (t + 2)2 − 5.

Zauważmy teraz, że

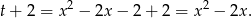
t+ 2 = x2 − 2x − 2 + 2 = x2 − 2x .

Zatem 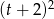(t+ 2 )2 może być dowolną liczbą z przedziału 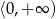⟨0,+ ∞ ) , czyli zbiorem wartości funkcji 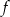jest przedział ⟨− 5,+ ∞ ) .
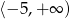Odpowiedź:

Rozwiązanie Losuj ponownie