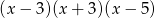/Szkoła średnia/Funkcje/Wielomiany/Stopnia 3/Rozkład

Zadanie nr 9012599

Dany jest wielomian 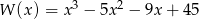3 2 W (x) = x − 5x − 9x + 45 .

  • Sprawdź, czy punkt 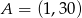A = (1,3 0) należy do wykresu tego wielomianu.
  • Zapisz wielomian 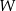W w postaci iloczynu trzech wielomianów stopnia pierwszego.
Wersja PDF

Rozwiązanie

  • Musimy sprawdzić, czy 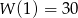W (1) = 30 . Liczymy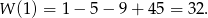
    W (1 ) = 1− 5− 9+ 45 = 32.

     
    Odpowiedź: Nie, nie należy

  •  

    Sposób I

    Szukamy pierwiastka wymiernego podanego wielomianu. Można sprawdzić, że takim pierwiastkiem jest 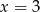x = 3 . Dzielimy teraz podany wielomian przez dwumian 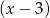(x− 3) . Robimy to jak kto umie, dzielenie wielomianów, schemat Hornera lub grupowanie wyrazów. My zrobimy to tą ostanią metodą.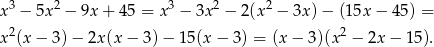

    x3 − 5x2 − 9x + 45 = x3 − 3x2 − 2(x2 − 3x) − (15x − 4 5) = x2(x − 3) − 2x(x − 3 )− 1 5(x− 3) = (x − 3)(x2 − 2x − 1 5).

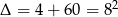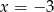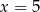    Pozostało rozłożyć trójmian kwadratowy w nawiasie, 2 Δ = 4 + 60 = 8 , x = − 3 lub x = 5 . Zatem podany wielomian możemy zapisać w postaci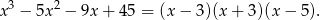

    x3 − 5x2 − 9x + 45 = (x − 3 )(x+ 3)(x− 5).

    Sposób II

    Jeżeli ktoś ma sokoli wzrok, to może szukany rozkład zobaczyć od ręki

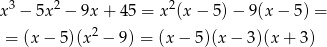
    x3 − 5x 2 − 9x + 4 5 = x2(x − 5) − 9(x − 5) = = (x − 5)(x 2 − 9 ) = (x− 5)(x − 3)(x + 3)

     
    Odpowiedź: (x− 3)(x + 3)(x − 5)

Wersja PDF
Rozwiązanie Losuj ponownie