Zbadaj, czy istnieje taka wartość współczynnika  , dla której wielomiany
, dla której wielomiany 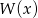 i
i ![[Q (x)]2](https://img.zadania.info/zad/4602131/HzadT2x.gif) są równe, jeśli
są równe, jeśli 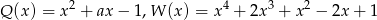 .
.
/Szkoła średnia/Funkcje/Wielomiany
Wyznacz wszystkie argumenty  , w których funkcja
, w których funkcja 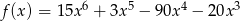 ma ekstrema lokalne.
ma ekstrema lokalne.
Wyznacz wartość największą i najmniejszą funkcji 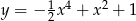 w przedziale
w przedziale 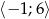 .
.
Rozłóż na czynniki drugiego stopnia wielomian 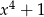 .
.
Rozłóż wielomian 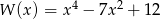 na czynniki liniowe. Podaj niewymierne pierwiastki tego wielomianu.
na czynniki liniowe. Podaj niewymierne pierwiastki tego wielomianu.
Wyznacz resztę z dzielenia wielomianu 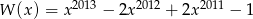 przez wielomian
przez wielomian 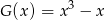 .
.
Rozłóż wielomian 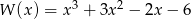 na czynniki liniowe.
na czynniki liniowe.
W wyniku dzielenia wielomianu 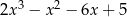 przez dwumian
przez dwumian 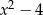 otrzymujemy resztę postaci
otrzymujemy resztę postaci 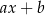 . Oblicz
. Oblicz  i
i 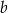 .
.
Dla jakich wartości parametru 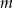 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu
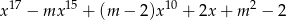
przez dwumian 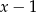 jest równa 3?
jest równa 3?
Dla jakich wartości parametru 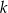 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu
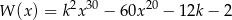
przez dwumian 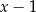 jest równa 2?
jest równa 2?
Reszta z dzielenia wielomianu 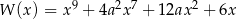 przez dwumian
przez dwumian 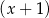 jest równa 2. Oblicz resztę z dzielenia wielomianu
jest równa 2. Oblicz resztę z dzielenia wielomianu 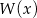 przez dwumian
przez dwumian 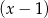 .
.
Funkcja 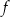 jest określona wzorem
jest określona wzorem
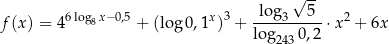
dla każdej liczby ![[ ] x ∈ 1,3 2](https://img.zadania.info/zad/5459831/HzadT2x.png) . Wyznacz zbiór wartości funkcji
. Wyznacz zbiór wartości funkcji 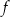 .
.
Wielomian 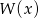 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 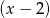 ,
, 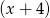 daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu
daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu 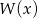 przez wielomian
przez wielomian 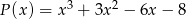 , wiedząc, że liczba -1 jest miejscem zerowym wielomianu
, wiedząc, że liczba -1 jest miejscem zerowym wielomianu 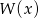 .
.
Wykaż, że funkcja 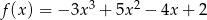 nie ma ekstremum.
nie ma ekstremum.
Wielomian 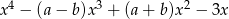 jest podzielny przez wielomian
jest podzielny przez wielomian 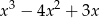 . Oblicz
. Oblicz  i
i 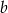 .
.
Przy dzieleniu wielomianu 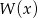 przez dwumian
przez dwumian 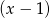 otrzymujemy iloraz
otrzymujemy iloraz 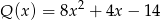 oraz resztę
oraz resztę 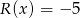 . Oblicz pierwiastki wielomianu
. Oblicz pierwiastki wielomianu 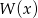 .
.
Reszta z dzielenia wielomianu 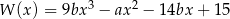 przez trójmian
przez trójmian 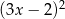 wynosi 3. Oblicz
wynosi 3. Oblicz  i
i 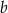 . Dla wyznaczonych wartości
. Dla wyznaczonych wartości  i
i 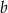 rozwiąż nierówność
rozwiąż nierówność 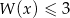 .
.
Wielomian 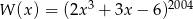 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 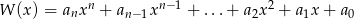 . Oblicz sumę
. Oblicz sumę 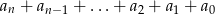 .
.
Niech ciąg 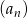 , dla
, dla 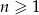 , będzie resztą z dzielenia wielomianu
, będzie resztą z dzielenia wielomianu 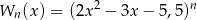 przez dwumian
przez dwumian 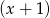 . Oblicz sumę dziesięciu początkowych wyrazów ciągu
. Oblicz sumę dziesięciu początkowych wyrazów ciągu 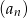 .
.
Wyznacz te argumenty, dla których funkcja 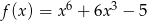 osiąga wartość najmniejszą.
osiąga wartość najmniejszą.
Reszta z dzielenia wielomianu 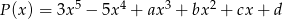 przez wielomian
przez wielomian 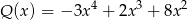 jest taka sama jak reszta z dzielenia wielomianu
jest taka sama jak reszta z dzielenia wielomianu 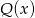 przez wielomian
przez wielomian 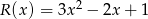 . Oblicz wartości współczynników
. Oblicz wartości współczynników 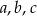 i
i 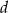 .
.

