Reszta z dzielenia wielomianu 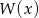 przez wielomian
przez wielomian 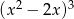 jest równa
jest równa 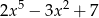 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 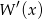 przez dwumian
przez dwumian 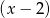 .
.
/Szkoła średnia/Funkcje/Wielomiany
Reszta z dzielenia wielomianu 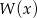 przez
przez 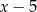 jest równa 4. Oblicz resztę z dzielenia wielomianu
jest równa 4. Oblicz resztę z dzielenia wielomianu 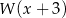 przez wielomian
przez wielomian 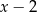 .
.
Reszta z dzielenia wielomianu 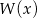 przez
przez 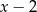 jest równa 7. Oblicz resztę z dzielenia wielomianu
jest równa 7. Oblicz resztę z dzielenia wielomianu 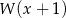 przez wielomian
przez wielomian 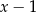 .
.
Wyznacz współczynniki 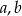 wielomianu
wielomianu 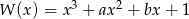 wiedząc, że dla każdego
wiedząc, że dla każdego 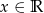 prawdziwa jest równość:
prawdziwa jest równość: 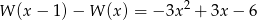 .
.
Wielomiany 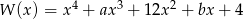 oraz
oraz 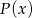 są wielomianami o współczynnikach całkowitych, przy czym
są wielomianami o współczynnikach całkowitych, przy czym ![W (x ) = [P (x)]2](https://img.zadania.info/zad/3139795/HzadT2x.gif) . Wyznacz wszystkie możliwe wartości
. Wyznacz wszystkie możliwe wartości  i
i 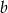 .
.
Wielomiany 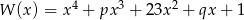 oraz
oraz 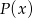 są wielomianami o współczynnikach całkowitych, przy czym
są wielomianami o współczynnikach całkowitych, przy czym ![W (x ) = [P (x)]2](https://img.zadania.info/zad/1984880/HzadT2x.gif) . Wyznacz wszystkie możliwe wartości
. Wyznacz wszystkie możliwe wartości 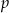 i
i 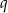 .
.
Wielomian 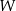 jest wielomianem stopnia 5 i spełnia warunki:
jest wielomianem stopnia 5 i spełnia warunki: 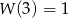 oraz
oraz 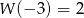 . Wykaż, że nie wszystkie współczynniki wielomianu
. Wykaż, że nie wszystkie współczynniki wielomianu 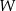 są liczbami całkowitymi.
są liczbami całkowitymi.
Reszta z dzielenia wielomianu 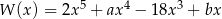 przez trójmian
przez trójmian 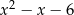 jest równa
jest równa 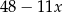 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 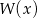 przez trójmian
przez trójmian 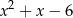 .
.
Wyznacz wszystkie wartości parametrów 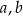 i
i  , dla których wielomian
, dla których wielomian
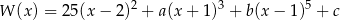
jest podzielny przez wielomian 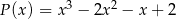 .
.
Wielomian 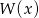 stopnia 3 jest podzielny przez trójmian kwadratowy
stopnia 3 jest podzielny przez trójmian kwadratowy 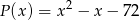 . Wiadomo ponadto, że
. Wiadomo ponadto, że 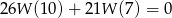 . Wyznacz miejsca zerowe wielomianu
. Wyznacz miejsca zerowe wielomianu 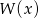 .
.
Funkcja 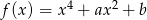 przyjmuje wartość 1 dla czterech argumentów:
przyjmuje wartość 1 dla czterech argumentów:
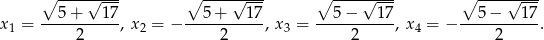
Oblicz najmniejszą wartość tej funkcji.
Reszta z dzielenia wielomianu 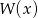 przez trójmian kwadratowy
przez trójmian kwadratowy 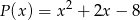 jest równa
jest równa 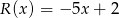 . Wyznacz resztę z dzielenia tego wielomianu przez dwumian
. Wyznacz resztę z dzielenia tego wielomianu przez dwumian 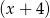 .
.
Dla jakich wartości parametru 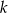 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 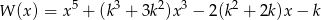 przez dwumian
przez dwumian 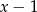 jest nie większa od (–2)?
jest nie większa od (–2)?
Wielomian 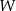 dany jest wzorem
dany jest wzorem 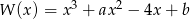 .
.
- Wyznacz
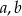 oraz
oraz  tak, aby wielomian
tak, aby wielomian 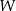 był równy wielomianowi
był równy wielomianowi 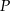 , gdy
, gdy 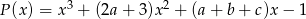 .
. - Dla
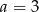 i
i 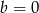 zapisz wielomian
zapisz wielomian 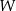 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.
Wyznacz zbiór wartości funkcji 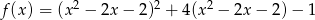 .
.
Dany jest wielomian 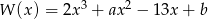 . Liczba 3 jest jednym z pierwiastków tego wielomianu. Reszta z dzielenia wielomianu
. Liczba 3 jest jednym z pierwiastków tego wielomianu. Reszta z dzielenia wielomianu 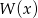 przez
przez 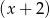 jest równa 20. Oblicz współczynniki
jest równa 20. Oblicz współczynniki  i
i 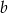 oraz pozostałe pierwiastki wielomianu
oraz pozostałe pierwiastki wielomianu 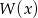 .
.
Reszta z dzielenia wielomianu 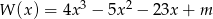 przez dwumian
przez dwumian 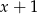 jest równa 20. Oblicz wartość współczynnika
jest równa 20. Oblicz wartość współczynnika 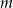 oraz pierwiastki tego wielomianu.
oraz pierwiastki tego wielomianu.
Reszta z dzielenia wielomianu 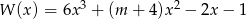 przez dwumian
przez dwumian 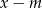 jest równa 8. Oblicz wartość
jest równa 8. Oblicz wartość 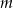 oraz pierwiastki tego wielomianu.
oraz pierwiastki tego wielomianu.
Maksymalny przedział, na którym funkcja 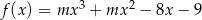 jest malejąca ma długość 2. Oblicz wartość parametru
jest malejąca ma długość 2. Oblicz wartość parametru 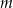 oraz wyznacz największą wartość funkcji na przedziale
oraz wyznacz największą wartość funkcji na przedziale 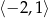 .
.
Oblicz najmniejszą wartość wielomianu 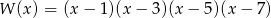 .
.
Reszty z dzielenia wielomianu 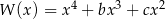 przez dwumiany
przez dwumiany 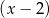 i
i 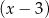 są odpowiednio równe
są odpowiednio równe 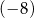 oraz
oraz 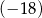 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 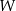 przez dwumian
przez dwumian 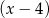 .
.
Dla jakich wartości parametru  , wielomian
, wielomian 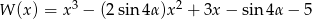 jest podzielny przez dwumian
jest podzielny przez dwumian 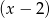 ?
?
Wyznacz przedziały monotoniczności funkcji 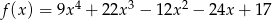 .
.

