Liczby 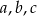 mają tę własność, że każdy z ciągów:
mają tę własność, że każdy z ciągów: 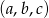 ,
, 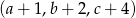 i
i 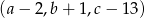 jest ciągiem geometrycznym. Oblicz
jest ciągiem geometrycznym. Oblicz 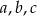 .
.
/Szkoła średnia/Ciągi/Geometryczny/Trzywyrazowy
Funkcje 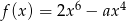 ,
, 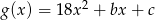 i
i 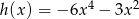 mają tę własność, że dla każdej liczby rzeczywistej
mają tę własność, że dla każdej liczby rzeczywistej 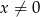 , liczby
, liczby 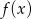 ,
, 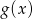 i
i 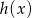 tworzą (w pewnej ustalonej kolejności) ciąg geometryczny. Wykaż, że funkcja
tworzą (w pewnej ustalonej kolejności) ciąg geometryczny. Wykaż, że funkcja 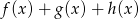 jest rosnąca na przedziale
jest rosnąca na przedziale 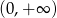 .
.
Liczby 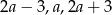 , w podanej kolejności, tworzą ciąg geometryczny. Wyznacz
, w podanej kolejności, tworzą ciąg geometryczny. Wyznacz  .
.
Trójwyrazowy ciąg 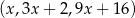 jest geometryczny. Oblicz
jest geometryczny. Oblicz  .
.
Dany jest trzywyrazowy ciąg 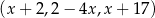 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Dany jest trzywyrazowy ciąg 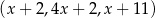 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Trzy liczby dodatnie 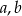 i
i  tworzą ciąg geometryczny. Suma tych liczb jest równa 26, a suma ich odwrotności wynosi
tworzą ciąg geometryczny. Suma tych liczb jest równa 26, a suma ich odwrotności wynosi 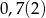 . Znajdź te liczby.
. Znajdź te liczby.
Rozwiąż układ równań:
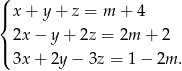
Dla jakich wartości parametru 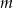 liczby
liczby 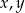 i
i  są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?
Suma trzech liczb tworzących ciąg geometryczny jest równa 26, a ich iloczyn jest równy 216. Wyznacz ten ciąg.
Trzy liczby dodatnie tworzą rosnący ciąg geometryczny o sumie równej 62. Suma logarytmów dziesiętnych tych liczb jest równa 3. Wyznacz te liczby.
Suma trzech liczb tworzących ciąg geometryczny jest równa 63, a ich iloczyn jest równy 5832. Wyznacz ten ciąg.
Wyznacz trzywyrazowy ciąg geometryczny, w którym suma trzech kolejnych wyrazów jest równa 84, a ich iloczyn jest równy 13824.
Trzywyrazowy ciąg geometryczny jest rosnący. Iloczyn wszystkich wyrazów tego ciągu jest równy -8, a iloraz pierwszego wyrazu przez trzeci wynosi 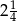 . Wyznacz ten ciąg.
. Wyznacz ten ciąg.
Ciąg 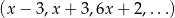 jest nieskończonym ciągiem geometrycznym o wyrazach dodatnich. Oblicz iloraz tego ciągu i uzasadnij, że
jest nieskończonym ciągiem geometrycznym o wyrazach dodatnich. Oblicz iloraz tego ciągu i uzasadnij, że 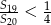 , gdzie
, gdzie 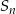 oznacza sumę
oznacza sumę  początkowych wyrazów tego ciągu.
początkowych wyrazów tego ciągu.
Trzy książki, których ceny tworzą ciąg geometryczny zakupiono płacąc łącznie 76 zł. Najdroższa z nich kosztowała o 4 zł mniej niż dwie pozostałe razem. Ile kosztowała każda książka?

