Dany jest trójkąt równoramienny 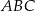 , w którym
, w którym 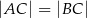 oraz
oraz 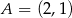 i
i 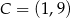 . Podstawa
. Podstawa 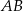 tego trójkąta jest zawarta w prostej
tego trójkąta jest zawarta w prostej 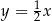 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 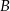 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt
Punkty 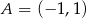 i
i 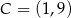 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 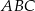 , w którym
, w którym 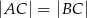 . Podstawa
. Podstawa 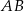 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 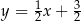 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 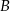 tego trójkąta.
tego trójkąta.
Boki trójkąta 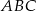 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 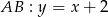 ,
, 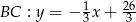 i
i 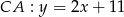 . Wyznacz współrzędne środka okręgu opisanego na trójkącie
. Wyznacz współrzędne środka okręgu opisanego na trójkącie 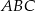 .
.
Dany jest trójkąt równoboczny 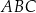 , w którym
, w którym 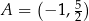 . Bok
. Bok 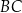 tego trójkąta jest zwarty w prostej o równaniu
tego trójkąta jest zwarty w prostej o równaniu 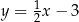 . Oblicz współrzędne środka odcinka
. Oblicz współrzędne środka odcinka 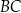 oraz oblicz pole trójkąta
oraz oblicz pole trójkąta 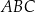 .
.
W trójkącie 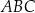 , w którym
, w którym 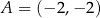 oraz
oraz 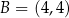 , kąt przy wierzchołku
, kąt przy wierzchołku 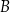 jest rozwarty. Bok
jest rozwarty. Bok 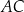 zawiera się w prostej
zawiera się w prostej 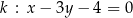 . Środek okręgu opisanego na trójkącie
. Środek okręgu opisanego na trójkącie 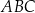 znajduje się w odległości
znajduje się w odległości 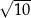 od boku
od boku 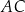 . Wyznacz równanie tego okręgu.
. Wyznacz równanie tego okręgu.
W układzie współrzędnych na płaszczyźnie zaznaczono punkty 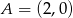 i
i 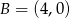 . Wyznacz wszystkie możliwe położenia punktu
. Wyznacz wszystkie możliwe położenia punktu 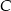 , dla których
, dla których 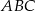 jest trójkątem równoramiennym o podstawie
jest trójkątem równoramiennym o podstawie 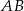 i polu równym 3.
i polu równym 3.
Znajdź równanie prostej 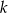 przechodzącej przez punkt
przechodzącej przez punkt 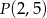 , która ogranicza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu równym 36.
, która ogranicza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu równym 36.
Napisz równanie okręgu opisanego na trójkącie o wierzchołkach 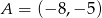 ,
, 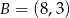 i
i 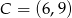 .
.
Dane są punkty 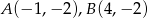 oraz
oraz 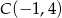 .
.
- Za pomocą odpowiedniego układu nierówności opisz trójkąt
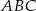 .
. - Oblicz odległość punktu
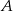 od prostej
od prostej 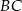 .
. - Oblicz promień koła wpisanego w trójkąt
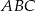 .
. - Wyznacz równanie symetralnej boku
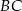 .
.
Punkty 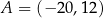 i
i 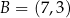 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 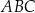 , w którym
, w którym 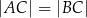 . Wierzchołek
. Wierzchołek 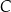 leży na osi
leży na osi 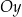 układu współrzędnych. Oblicz współrzędne wierzchołka
układu współrzędnych. Oblicz współrzędne wierzchołka 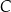 oraz obwód tego trójkąta.
oraz obwód tego trójkąta.
W kartezjańskim układzie współrzędnych  punkty
punkty 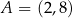 oraz
oraz 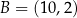 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 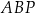 , w którym
, w którym 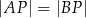 . Wierzchołek
. Wierzchołek 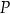 leży na osi
leży na osi 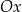 układu współrzędnych. Oblicz współrzędne punktu
układu współrzędnych. Oblicz współrzędne punktu 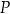 oraz długość odcinka
oraz długość odcinka 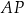 .
.
Punkty 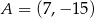 i
i 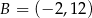 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 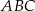 , w którym
, w którym 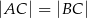 . Wierzchołek
. Wierzchołek 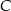 leży na prostej
leży na prostej 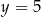 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 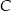 oraz obwód tego trójkąta.
oraz obwód tego trójkąta.
Punkty 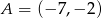 i
i 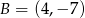 są wierzchołkami podstawy trójkąta równoramiennego
są wierzchołkami podstawy trójkąta równoramiennego 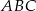 , a wysokość opuszczona z wierzchołka
, a wysokość opuszczona z wierzchołka 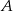 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 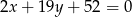 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 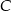 .
.
Punkty 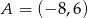 i
i 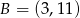 są wierzchołkami podstawy trójkąta równoramiennego
są wierzchołkami podstawy trójkąta równoramiennego 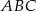 , a wysokość opuszczona z wierzchołka
, a wysokość opuszczona z wierzchołka 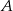 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 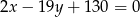 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 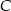 .
.
Okrąg wpisany w trójkąt 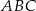 ma równanie
ma równanie 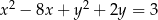 . Oblicz
. Oblicz 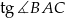 jeżeli
jeżeli 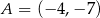 .
.
Punkty 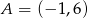 i
i 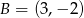 są wierzchołkami trójkąta
są wierzchołkami trójkąta 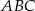 . Wiedząc, że punkt przecięcia się wysokości tego trójkąta ma współrzędne
. Wiedząc, że punkt przecięcia się wysokości tego trójkąta ma współrzędne 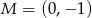 oblicz współrzędne wierzchołka
oblicz współrzędne wierzchołka 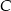 .
.
Oblicz pole trójkąta o wierzchołkach: 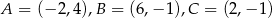 .
.
Oblicz pole trójkąta o wierzchołkach: 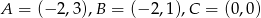 .
.
W trójkącie równobocznym 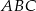 dane są wierzchołek
dane są wierzchołek 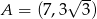 i środek okręgu wpisanego
i środek okręgu wpisanego 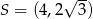 . Oblicz pole trójkąta
. Oblicz pole trójkąta 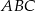 .
.
Punkt 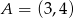 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 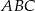 , o kącie prostym
, o kącie prostym 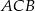 , a
, a 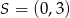 jest środkiem okręgu opisanego na tym trójkącie. Wyznacz współrzędne pozostałych wierzchołków tego trójkąta, wiedząc, że
jest środkiem okręgu opisanego na tym trójkącie. Wyznacz współrzędne pozostałych wierzchołków tego trójkąta, wiedząc, że 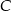 należy do ujemnej części osi
należy do ujemnej części osi 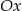 .
.
Na rysunku prosta 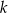 przechodzi przez punkt
przechodzi przez punkt 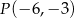 .
.
Wiedząc, że stosunek pól zacieniowanych trójkątów prostokątnych jest równy 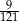
- oblicz pola tych trójkątów;
- wyznacz równanie prostej
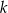 .
.
Punkty 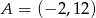 i
i 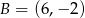 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 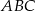 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 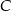 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 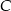 tego trójkąta, wiedząc, że leży on na prostej o równaniu
tego trójkąta, wiedząc, że leży on na prostej o równaniu 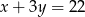 . Sporządź rysunek w prostokątnym układzie współrzędnych. Rozważ wszystkie przypadki.
. Sporządź rysunek w prostokątnym układzie współrzędnych. Rozważ wszystkie przypadki.
Punkty 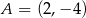 ,
, 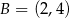 i
i 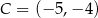 są wierzchołkami trójkąta
są wierzchołkami trójkąta 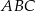 . Napisz równanie prostej zawierającej tą średnicę okręgu opisanego na trójkącie
. Napisz równanie prostej zawierającej tą średnicę okręgu opisanego na trójkącie 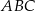 , której końcem jest punkt
, której końcem jest punkt 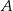 .
.
Napisz równanie prostopadłej opuszczonej z wierzchołka 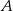 trójkąta
trójkąta 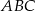 o wierzchołkach
o wierzchołkach 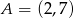 ,
, 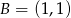 i
i 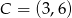 na środkową
na środkową 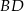 boku
boku 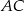 .
.
W trójkącie prostokątnym 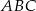 o przeciwprostokątnej
o przeciwprostokątnej 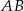 dane są wierzchołki
dane są wierzchołki 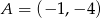 i
i 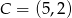 . Punkt
. Punkt 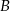 leży na prostej o równaniu
leży na prostej o równaniu 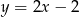 . Wyznacz równanie okręgu opisanego na tym trójkącie.
. Wyznacz równanie okręgu opisanego na tym trójkącie.

