Wyznacz współrzędne wierzchołków trójkąta, którego boki zawarte są w prostych o równaniach 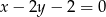 ,
, 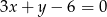 ,
, 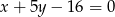 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt
Dany jest trójkąt 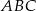 , gdzie
, gdzie 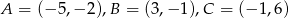 .
.
- Wyznacz równanie prostej zawierającej bok
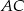 .
. - Oblicz długość środkowej
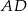 .
. - Wyznacz równanie prostej zawierającej wysokość poprowadzoną z wierzchołka
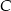 .
. - Oblicz pole tego trójkąta.
Dany jest trójkąt 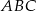 , gdzie
, gdzie 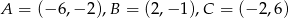 .
.
- Wyznacz równanie prostej zawierającej bok
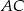 .
. - Oblicz długość środkowej
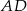 .
. - Wyznacz równanie prostej zawierającej wysokość poprowadzoną z wierzchołka
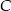 .
. - Oblicz pole tego trójkąta.
Dwa boki trójkąta prostokątnego 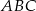 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 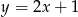 oraz
oraz 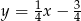 . Wyznacz współrzędne wierzchołków trójkąta
. Wyznacz współrzędne wierzchołków trójkąta 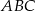 jeżeli wiadomo, że jego trzeci bok jest zawarty w prostej przechodzącej przez punkt
jeżeli wiadomo, że jego trzeci bok jest zawarty w prostej przechodzącej przez punkt 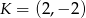 . Rozważ wszystkie możliwości.
. Rozważ wszystkie możliwości.
Sprawdź czy punkt 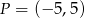 jest środkiem okręgu wpisanego w trójkąt o wierzchołkach
jest środkiem okręgu wpisanego w trójkąt o wierzchołkach 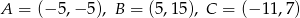 .
.
Podstawa trójkąta równoramiennego zawiera się w prostej 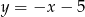 , a jedno z jego ramion w prostej
, a jedno z jego ramion w prostej 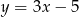 . Wyznacz równanie drugiego ramienia tego trójkąta, jeżeli jednym z jego wierzchołków jest punkt o współrzędnych
. Wyznacz równanie drugiego ramienia tego trójkąta, jeżeli jednym z jego wierzchołków jest punkt o współrzędnych 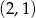 .
.
Prosta o równaniu 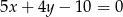 przecina oś
przecina oś 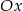 układu współrzędnych w punkcie
układu współrzędnych w punkcie 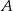 oraz oś
oraz oś 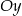 w punkcie
w punkcie 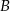 . Oblicz współrzędne wszystkich punktów
. Oblicz współrzędne wszystkich punktów 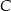 leżących na osi
leżących na osi 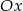 i takich, że trójkąt
i takich, że trójkąt 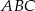 ma pole równe 35 .
ma pole równe 35 .
Podstawa 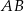 trójkąta równoramiennego
trójkąta równoramiennego 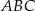 zawarta jest w prostej
zawarta jest w prostej 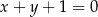 . Ramię
. Ramię 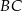 zawiera się w prostej
zawiera się w prostej 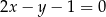 . Wyznacz równanie prostej
. Wyznacz równanie prostej 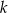 , zawierającej ramię
, zawierającej ramię 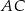 , wiedząc że punkt
, wiedząc że punkt 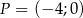 należy do prostej
należy do prostej 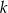 .
.
Punkty 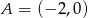 i
i 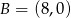 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 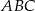 o przeciwprostokątnej
o przeciwprostokątnej 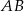 i polu równym 15. Oblicz współrzędne punktu
i polu równym 15. Oblicz współrzędne punktu 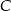 .
.
W okrąg o równaniu 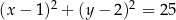 wpisano trójkąt
wpisano trójkąt 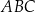 . Bok
. Bok 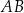 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 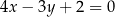 . Wysokość
. Wysokość 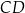 tego trójkąta dzieli bok
tego trójkąta dzieli bok 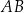 tak, że
tak, że 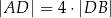 . Oblicz pole trójkąta
. Oblicz pole trójkąta 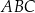 .
.
Punkt 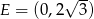 jest środkiem boku
jest środkiem boku 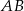 trójkąta równobocznego
trójkąta równobocznego 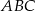 , prosta
, prosta 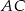 ma równanie
ma równanie 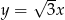 , a początek układu współrzędnych pokrywa się wierzchołkiem
, a początek układu współrzędnych pokrywa się wierzchołkiem 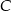 tego trójkąta. Napisz równania wysokości trójkąta
tego trójkąta. Napisz równania wysokości trójkąta 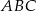 przechodzących przez wierzchołki
przechodzących przez wierzchołki 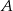 i
i 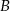 .
.
Punkt 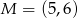 jest środkiem ramienia
jest środkiem ramienia 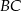 trójkąta równoramiennego
trójkąta równoramiennego 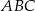 , w którym
, w którym 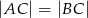 . Podstawa
. Podstawa  tego trójkąta jest zawarta w prostej o równaniu
tego trójkąta jest zawarta w prostej o równaniu 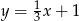 oraz
oraz 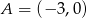 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 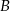 tego trójkąta.
tego trójkąta.
Punkt 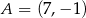 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 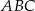 , w którym
, w którym 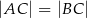 . Obie współrzędne wierzchołka
. Obie współrzędne wierzchołka 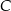 są liczbami ujemnymi. Okrąg wpisany w trójkąt
są liczbami ujemnymi. Okrąg wpisany w trójkąt 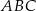 ma równanie
ma równanie 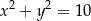 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 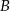 i
i 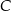 tego trójkąta.
tego trójkąta.
Punkt 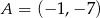 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 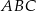 , w którym
, w którym 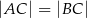 . Obie współrzędne wierzchołka
. Obie współrzędne wierzchołka 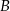 są liczbami dodatnimi. Okrąg wpisany w trójkąt
są liczbami dodatnimi. Okrąg wpisany w trójkąt 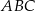 ma równanie
ma równanie 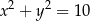 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 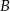 i
i 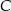 tego trójkąta.
tego trójkąta.
Punkty 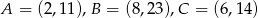 są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka 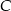 przecina prostą
przecina prostą 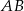 w punkcie
w punkcie 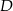 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 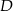 .
.
Punkty 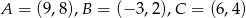 są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka 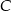 przecina prostą
przecina prostą 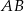 w punkcie
w punkcie 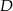 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 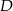 .
.
W układzie współrzędnych są dane punkty 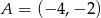 ,
, 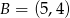 .
.
- Oblicz odległość punktu
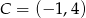 od prostej przechodzącej przez punkty
od prostej przechodzącej przez punkty 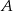 i
i 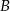 .
. - Uzasadnij, że jeśli
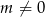 , to punkty
, to punkty 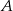 ,
, 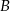 oraz punkt
oraz punkt 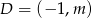 są wierzchołkami trójkąta.
są wierzchołkami trójkąta.
Oblicz promień okręgu opisanego na trójkącie o wierzchołkach 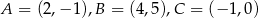 .
.
Uzasadnij, że koło o środku 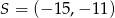 i promieniu
i promieniu 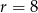 jest w całości zawarte w trójkącie o wierzchołkach
jest w całości zawarte w trójkącie o wierzchołkach 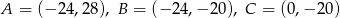 .
.
Punkty 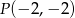 ,
, 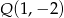 i
i 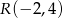 są środkami boków
są środkami boków 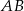 ,
, 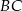 i
i 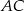 trójkąta
trójkąta 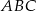 . Oblicz:
. Oblicz:
- Współrzędne wierzchołków trójkąta
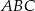 .
. - Obwód trójkąta
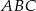 .
.
Rozstrzygnij czy trójkąt 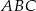 i trójkąt
i trójkąt 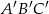 są przystające jeśli współrzędne ich wierzchołków to
są przystające jeśli współrzędne ich wierzchołków to 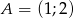 ,
, 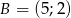 ,
, 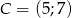 ,
, 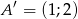 ,
, 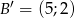 ,
, 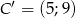 .
.
Punkty 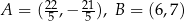 oraz
oraz 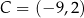 są wierzchołkami trójkąta
są wierzchołkami trójkąta 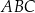 . Symetralna boku
. Symetralna boku 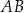 tego trójkąta przecina bok
tego trójkąta przecina bok 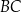 w punkcie
w punkcie 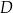 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 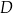 .
.
Odległość każdego z wierzchołków 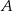 i
i 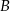 trójkąta
trójkąta 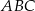 od punktu
od punktu 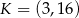 jest równa
jest równa 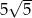 , a odległość tych wierzchołków od punktu
, a odległość tych wierzchołków od punktu 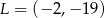 jest równa 25. Okrąg opisany na trójkącie
jest równa 25. Okrąg opisany na trójkącie 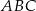 jest styczny do prostej
jest styczny do prostej 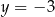 w punkcie
w punkcie 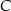 . Punkt
. Punkt 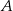 znajduje się w pierwszej ćwiartce układu współrzędnych. Wyznacz współrzędne wierzchołków trójkąta
znajduje się w pierwszej ćwiartce układu współrzędnych. Wyznacz współrzędne wierzchołków trójkąta 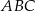 .
.

