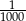Uczeń ma 2009 sześciennych klocków o krawędzi długości 1 oraz 2009 kolorowych kwadratowych naklejek o boku długości 1. Uczeń ten skleił ze wszystkich klocków prostopadłościan i okleił całą jego powierzchnię naklejkami, przyklejając dokładnie po jednej do każdej ściany klocka, tworzącej tę powierzchnię. Okazało się, że uczniowi pozostały jeszcze naklejki. Ile ich pozostało?
A) Więcej niż 1000 B) 763 C) 476 D) 49 E) Opisana sytuacja jest niemożliwa
/Konkursy/Zadania testowe/Geometria
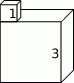
Bryła widoczna na rysunku obok jest zbudowana z dwóch sześcianów o krawędziach długości 1 cm i 3 cm. Jakie jest pole powierzchni tej bryły?
A) 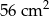 B)
B) 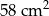 C)
C) 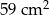 D)
D) 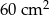 E)
E) 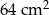
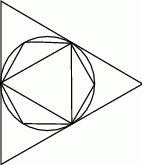
Trójkąt równoboczny i sześciokąt foremny wpisano w okrąg, na którym opisano trójkąt równoboczny (patrz rysunek). Niech 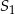 oznacza pole dużego trójkąta,
oznacza pole dużego trójkąta, 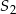 pole małego trójkąta, a
pole małego trójkąta, a 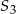 pole sześciokąta foremnego. Która z równości jest prawdziwa?
pole sześciokąta foremnego. Która z równości jest prawdziwa?
A) 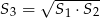 B)
B) 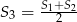 C)
C) 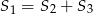 D)
D) 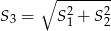 E)
E) 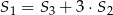
W kwadracie o boku długości 1 narysowano dwa okręgi jak na rysunku. Jaką wartość ma suma długości promieni tych okręgów?

A) 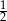
B) 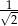
C) 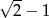
D) 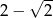
E) Suma ta zależy od stosunku promieni tych okręgów
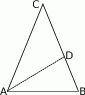
W trójkącie równoramiennym 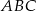 , w którym
, w którym 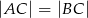 , poprowadzono dwusieczną
, poprowadzono dwusieczną 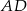 kąta przy wierzchołku
kąta przy wierzchołku 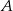 (patrz rysunek), przy czym
(patrz rysunek), przy czym 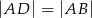 . Jaka jest miara kąta
. Jaka jest miara kąta 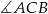 ?
?
A) 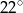 B)
B) 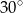 C)
C) 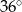 D)
D) 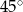 E)
E) 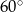
Na płaszczyźnie zaznaczono punkty 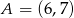 ,
, 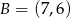 ,
, 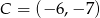 ,
, 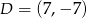 i
i 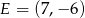 . Który z poniższych odcinków jest równoległy do osi
. Który z poniższych odcinków jest równoległy do osi 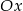 ?
?
A) 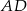 B)
B) 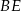 C)
C) 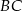 D)
D) 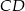 E)
E) 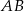
Pierścienie boromejskie to takie trzy pierścienie, których nie można rozdzielić bez rozcinania, ale po usunięciu któregokolwiek z nich pozostałe dwa nie są ze sobą powiązane w żaden sposób. Który z rysunków przedstawia pierścienie boromejskie?

Trójkąty 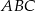 i
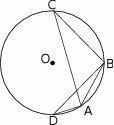
i 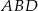 zostały wpisane w okrąg, jak na rysunku obok. Wiadomo, że
zostały wpisane w okrąg, jak na rysunku obok. Wiadomo, że 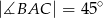 oraz
oraz 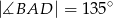 . Wówczas długości cięciw
. Wówczas długości cięciw 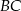 i
i 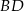 spełniają zależność
spełniają zależność
A) 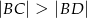
B) 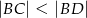
C) 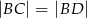
D) 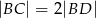
E) 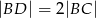
Na rysunku obok mały kwadrat wpisano w duży kwadrat. Pole małego kwadratu jest równe
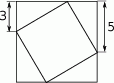
A) 16 B) 28 C) 34 D) 36 E) 49
W matematycznej pajęczynie na rysunku obok długości wszystkich odcinków wyrażają się liczbami całkowitymi. Ile jest równe  ?
?
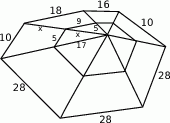
A) 11 B) 13 C) 15 D) 17 E) 19
Na rysunku obok dwa sześciokąty foremne mają wspólny bok. Jaka część pola równoległoboku jest zacieniowana?

A) 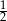 B)
B) 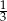 C)
C) 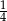 D)
D) 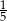 E)
E) 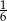
Na powierzchni piłki namalowano trzy jednakowe okręgi, dzielące ją na osiem jednakowych części, jak na rysunku obok. Trzmiel, który usiadł na piłce w punkcie przecięcia okręgów, wędruje po namalowanych okręgach w taki sposób, że po przejściu ćwiartki okręgu w punkcie przecięcia z innym okręgiem zawsze skręca na przemian w w prawo albo w lewo, tj. w prawo, gdy w poprzedzającym punkcie skręcał w lewo, natomiast w lewo, gdy w poprzedzającym punkcie skręcał w prawo. Jaka jest najmniejsza liczba ćwiartek okręgów, które musi przejść trzmiel aby ponownie znalazł się w punkcie, z którego wyruszył?
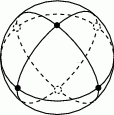
A) 6 B) 9 C) 12 D) 15 E) 18
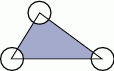
Pole trójkąta przedstawionego na rysunku jest równe 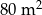 , a promień każdego okręgu w środku w jego wierzchołku jest równy 2 m. Ile metrów kwadratowych ma pole zacieniowanej figury?
, a promień każdego okręgu w środku w jego wierzchołku jest równy 2 m. Ile metrów kwadratowych ma pole zacieniowanej figury?
A) 76 B) 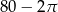 C)
C) 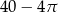 D)
D) 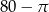 E)
E) 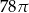
Na rysunku obok, trójkąt i kwadrat mają równe obwody. Ile wynosi obwód całej figury (pięciokąta)?
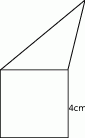
A) 12 cm B) 24 cm C) 28 cm D) 32 cm E) 20 cm
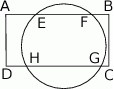
Okrąg przecina boki prostokąta 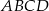 w punktach
w punktach 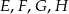 , jak na rysunku obok. Wiadomo, że
, jak na rysunku obok. Wiadomo, że 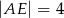 ,
, 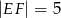 ,
, 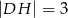 . Ile wynosi długość odcinka
. Ile wynosi długość odcinka 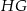 ?
?
A) 6 B) 7 C) 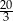 D) 8 E) 9
D) 8 E) 9
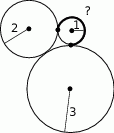
Rysunek obok przedstawia trzy wzajemnie styczne okręgi o promieniach 1,2 i 3. Jaka jest długość łuku zaznaczonego pogrubioną linią?
A) 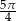 B)
B) 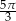 C)
C) 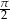 D)
D) 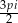 E)
E) 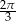
Kwadraty przedstawione na rysunku mają boki równe 1. Pole zacieniowanego czworokąta jest równe
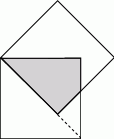
A) 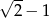 B)
B) 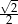 C)
C) 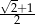 D)
D) 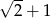 E)
E) 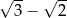
Mirek zmierzył kąty w dwóch trójkątach. Jeden z trójkątów był ostrokątny, a drugi rozwartokątny. Mirek zapamiętał miary czterech z tych katów 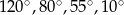 . Jaka jest miara najmniejszego kąta w trójkącie ostrokątnym?
. Jaka jest miara najmniejszego kąta w trójkącie ostrokątnym?
A) 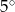 B)
B) 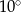 C)
C) 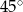 D)
D) 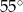 E) Nie można tego ustalić.
E) Nie można tego ustalić.
Jeden z boków trójkąta ma długość 120, drugi 130. Która z poniższych liczb nie może być długością trzeciego boku?
A) 40 B) 99 C) 100 D) 150 E) 260
Duży kwadrat o polu 1 został podzielony na kwadraty, jak na rysunku obok. Pole małego zacieniowanego kwadratu jest równe.

A) 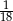 B)
B) 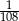 C)
C) 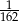 D)
D) 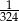 E)
E)