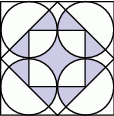
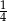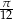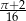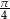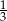W prostokącie umieszczono sześć identycznych okręgów, jak na rysunku. Wierzchołki małego prostokąta są środkami czterech z tych okręgów. Wiadomo, że obwód małego prostokąta jest równy 60 cm. Ile jest równy obwód dużego prostokąta?
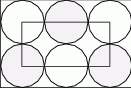
A) 90cm B) 140cm C)120 cm D)100 cm E)80 cm

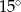
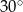
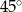
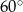
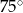
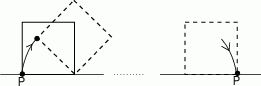
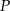 ponownie znajdzie się na tej prostej. Jaka jest długość drogi, którą zakreślił punkt
ponownie znajdzie się na tej prostej. Jaka jest długość drogi, którą zakreślił punkt 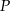 ?
? 
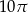
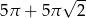
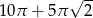
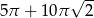
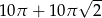
 będącego środkiem kwadratu
będącego środkiem kwadratu  (patrz rysunek) prowadzimy odcinki
(patrz rysunek) prowadzimy odcinki 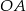 ,
, 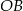 ,
, 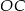 i
i 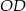 do boków tak, że
do boków tak, że 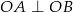 i
i 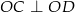 . Ile jest równe pole zacieniowanej części kwadratu, jeśli bok kwadratu ma długość 2?
. Ile jest równe pole zacieniowanej części kwadratu, jeśli bok kwadratu ma długość 2? 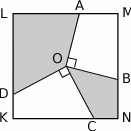
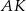 kąta
kąta 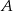 w trójkącie
w trójkącie 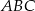 podzieliła ten trójkąt na dwa trójkąty o równych polach. Wówczas trójkąt
podzieliła ten trójkąt na dwa trójkąty o równych polach. Wówczas trójkąt 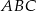 jest na pewno
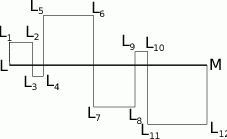
jest na pewno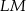 o długości 24 cm i przez odcinki łamanej
o długości 24 cm i przez odcinki łamanej 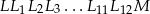 . Ile jest równa długość łamanej
. Ile jest równa długość łamanej 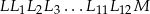 ?
? 
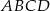 będzie kwadratem o boku 12 cm. Punkty
będzie kwadratem o boku 12 cm. Punkty 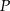 ,
, 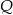 ,
, 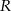 są odpowiednio środkami boków
są odpowiednio środkami boków 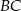 ,
,  ,
,  (rysunek obok). Pole zacieniowanego czworokąta jest równe
(rysunek obok). Pole zacieniowanego czworokąta jest równe 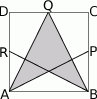
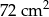
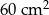
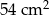
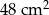
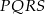 mamy
mamy 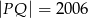 ,
, 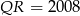 ,
, 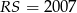 ,
, 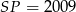 . Przy których wierzchołkach kąty wewnętrzne czworokąta mają zawsze miarę mniejszą niż
. Przy których wierzchołkach kąty wewnętrzne czworokąta mają zawsze miarę mniejszą niż 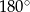 ?
?
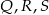
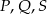
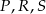
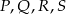

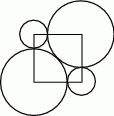
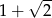
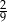
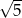
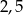
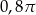

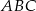 miara kąta wewnętrznego przy wierzchołku
miara kąta wewnętrznego przy wierzchołku 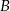 jest równa
jest równa 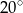 , a miara kąta wewnętrznego przy wierzchołku
, a miara kąta wewnętrznego przy wierzchołku 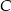 jest równa
jest równa 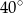 . Ponadto długość dwusiecznej kąta przy wierzchołku
. Ponadto długość dwusiecznej kąta przy wierzchołku 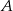 jest równa 2. Ile wynosi różnica
jest równa 2. Ile wynosi różnica 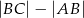 ?
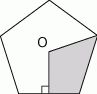
? jest środkiem pięciokąta foremnego. Jaką częścią pięciokąta jest zacieniowany obszar?
jest środkiem pięciokąta foremnego. Jaką częścią pięciokąta jest zacieniowany obszar?