Zadanie nr 6661225
Wyznacz wszystkie wartości parametru 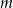 , dla których prosta o równaniu
, dla których prosta o równaniu 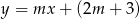 ma dokładnie dwa punkty wspólne z okręgiem o środku w punkcie
ma dokładnie dwa punkty wspólne z okręgiem o środku w punkcie 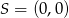 i promieniu
i promieniu 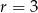 .
.
Rozwiązanie
Sposób I
Równanie okręgu opisanego w treści zadania to
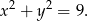
Aby wyznaczyć jego punkty wspólne z daną prostą podstawiamy w powyższym równaniu 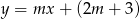 .
.
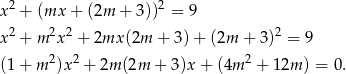
Otrzymane równanie to zwykłe równanie kwadratowe – jeżeli ma mieć dwa różne rozwiązania, to musi być 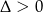 .
.
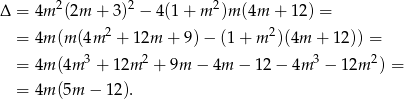
Rozwiązaniem nierówności 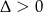 jest więc zbiór:
jest więc zbiór: 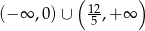 .
.
Sposób II
Jeżeli prosta ma przecinać okrąg w dwóch punktach, to środek tego okręgu musi być odległy od tej prostej o mniej niż promień okręgu. Korzystając ze wzoru na odległość punktu 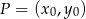 od prostej
od prostej 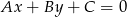 :
:
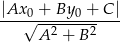
mamy w naszej sytuacji nierówność
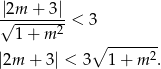
Ponieważ obie strony nierówności są nieujemne, możemy podnieść nierówność stronami do kwadratu i mamy
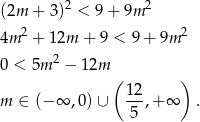
Odpowiedź: