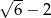/Szkoła średnia/Ciągi/Geometryczny/W geometrii

Zadanie nr 3872746

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie prostokątnym długości wysokości i środkowej poprowadzonej z wierzchołka kąta prostego oraz długość przeciwprostokątnej tworzą ciąg geometryczny, w którym iloczyn wyrazów jest równy 8. Oblicz promień okręgu wpisanego w ten trójkąt.

Rozwiązanie

Przyjmijmy oznaczenia jak na rysunku.

PIC

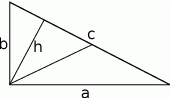
Ponieważ środek przeciwprostokątnej jest środkiem okręgu opisanego na trójkącie prostokątnym, to długość środkowej poprowadzonej z wierzchołka kąta prostego to długość promienia okręgu opisanego, czyli c 2 . Wiemy zatem, że liczby

c- h < 2 < c

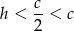
tworzą ciąg geometryczny oraz iloczyn tych liczb jest równy 8. W szczególności iloraz tego ciągu geometrycznego musi być równy 2, czyli 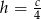h = c 4 oraz warunek z iloczynem daje nam

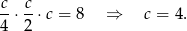
c- c- 4 ⋅ 2 ⋅ c = 8 ⇒ c = 4.

Stąd h = 1 i porównując wzory na pole mamy

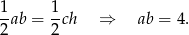
1-ab = 1-ch ⇒ ab = 4. 2 2

Zastanówmy się co musimy policzyć. Promień okręgu wpisanego wyliczymy ze wzoru

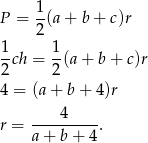
1 P = -(a + b + c)r 2 1ch = 1(a + b + c)r 2 2 4 = (a + b + 4)r r = ----4----. a + b + 4

Aby dokończyć ten rachunek musimy wyliczyć 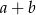a+ b . To nie jest jednak trudne, bo znamy 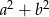a2 + b2 (twierdzenie Pitagorasa) i 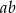ab . Liczymy

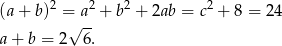
(a+ b )2 = a2 + b2 + 2ab = c2 + 8 = 24 √ -- a+ b = 2 6.

Stąd

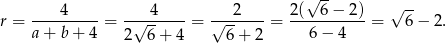
√ -- √ -- r = ----4---- = --√-4---- = √--2----= 2(--6-−-2)-= 6− 2. a+ b+ 4 2 6+ 4 6 + 2 6− 4

 
Odpowiedź: √ -- 6 − 2

Wersja PDF
Rozwiązanie Losuj ponownie