Zadanie nr 3067806
Podaj wzór na  -ty wyraz ciągu
-ty wyraz ciągu 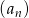 , jeżeli
, jeżeli 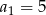 i
i 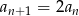 dla
dla 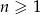 .
.
Rozwiązanie
Sposób I
Liczymy
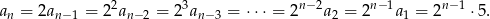
Ostatnie indeksy napisaliśmy korzystając z obserwacji, że wykładnik przy dwójce plus numer wyrazu dają w sumie  .
.
Sposób II
Ponieważ każdy kolejny wyraz podanego ciągu powstaje z poprzedniego przez przemnożenie przez 2, ciąg ten jest ciągiem geometrycznym o pierwszym wyrazie 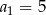 i ilorazie
i ilorazie 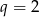 . Ze wzoru na
. Ze wzoru na  -ty wyraz ciągu geometrycznego mamy
-ty wyraz ciągu geometrycznego mamy
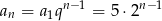
Odpowiedź: