Zadanie nr 3511342

Dane jest równanie z parametrem :

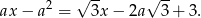
2 √ -- √ -- ax − a = 3x− 2a 3 + 3.

Dla jakich wartości parametru równanie ma jedno rozwiązanie? Wyznacz to rozwiązanie i przedstaw je w najprostszej postaci.

Rozwiązanie

Przekształcamy podane równanie

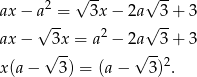
2 √ -- √ -- ax − a√ =- 3x − 2a√ 3-+ 3 ax − 3x = a2 − 2a 3 + 3 √ -- √ -- x (a− 3) = (a− 3)2.

Aby równanie miało dokładnie jedno rozwiązanie, musi być 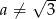√ -- a ⁄= 3 . Rozwiązanie to jest równe

-- x = a − √ 3.

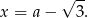
Odpowiedź: 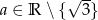√ -- a ∈ R ∖ { 3 } , √ -- x = a− 3