Funkcja 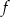 określona wzorem
określona wzorem 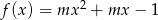 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 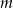 , dla których:
, dla których:
- funkcja
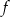 przyjmuje tylko wartości ujemne,
przyjmuje tylko wartości ujemne, - zbiorem wartości funkcji
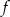 jest przedział
jest przedział 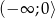 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Funkcja 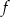 określona wzorem
określona wzorem 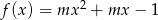 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 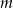 , dla których:
, dla których:
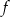 przyjmuje tylko wartości ujemne,
przyjmuje tylko wartości ujemne, 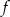 jest przedział
jest przedział 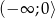 .
.Wyznacz współczynniki funkcji kwadratowej 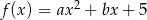 wiedząc, że
wiedząc, że 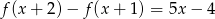 .
.
Dana jest funkcja 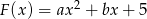 . Wyznacz
. Wyznacz  i
i 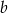 wiedząc, że
wiedząc, że 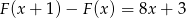 .
.
Wyznacz współczynniki funkcji kwadratowej 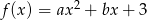 wiedząc, że
wiedząc, że 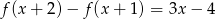 .
.
Funkcję kwadratową 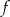 można opisać wzorem mającym postać
można opisać wzorem mającym postać 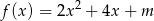 .
.
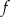 ma dwa różne pierwiastki
ma dwa różne pierwiastki 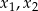 , a następnie oblicz
, a następnie oblicz 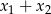 .
. 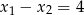 , oblicz
, oblicz 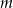 . Dla wyznaczonej liczby
. Dla wyznaczonej liczby 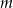 naszkicuj wykres funkcji
naszkicuj wykres funkcji 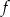 w układzie współrzędnych, a następnie rozwiąż równanie
w układzie współrzędnych, a następnie rozwiąż równanie 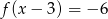 .
. 
Funkcja kwadratowa 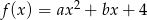 , osiąga wartości ujemne wtedy i tylko wtedy, gdy
, osiąga wartości ujemne wtedy i tylko wtedy, gdy 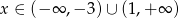 .
.
 i
i 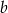 .
. 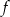 .
. 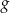 , której wykres otrzymamy przesuwając wykres funkcji
, której wykres otrzymamy przesuwając wykres funkcji 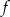 o wektor
o wektor ![→ u = [2,− 130]](https://img.zadania.info/zad/9353293/HzadT7x.gif) .
.  , dla których
, dla których 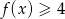 .
.Funkcja 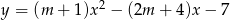 jest malejąca w zbiorze
jest malejąca w zbiorze 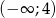 i rosnąca w zbiorze
i rosnąca w zbiorze 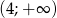 . Wyznacz parametr
. Wyznacz parametr 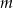 .
.
Dana jest funkcja 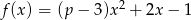 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 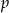 , dla których:
, dla których:
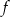 jest liczbą ujemną,
jest liczbą ujemną, 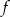 jest mniejsza od -2.
jest mniejsza od -2.Wyznacz wzór funkcji 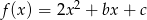 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 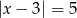 .
.
Wyznacz wzór funkcji 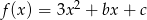 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 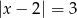 .
.
Wyznacz wszystkie całkowite wartości 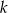 , dla których funkcja
, dla których funkcja 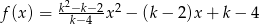 osiąga minimum i ma dwa różne miejsca zerowe.
osiąga minimum i ma dwa różne miejsca zerowe.
