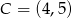/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Dowolny/Wyliczanie wierzchołków

Zadanie nr 3482505

Znając współrzędne wierzchołków trójkąta 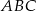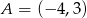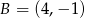ABC , A = (− 4,3 ) , B = (4 ,−1 ) oraz punkt przecięcia się jego wysokości 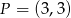P = (3,3) wyznacz współrzędne wierzchołka .

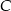Rozwiązanie

Jak zwykle zaczynamy od schamtycznego rysunku.

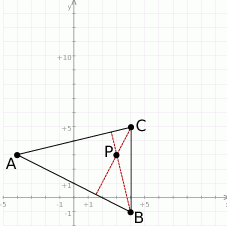
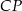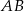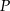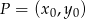
To co widać od razu, to że łatwo jest napisać równanie wysokości – jest to prosta prostopadła do i przechodząca przez . Najprościej jest skorzystać ze wzoru na prostą prostopadłą do wektora → v = [a,b] i przechodzącą przez punkt P = (x 0,y 0)

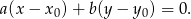
a(x − x0) + b(y − y0) = 0 .

W naszej sytuacji mamy → → v = AB = [8,− 4] . Zatem równanie prostej

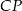
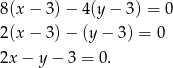
8(x − 3) − 4(y − 3) = 0 2(x − 3) − (y − 3) = 0 2x − y − 3 = 0.

Podobnie możemy napisać równanie boku 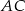– jest to prosta prostopadła do wektora → BP = [− 1,4] i przechodząca przez punkt A = (− 4,3) .

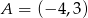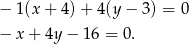
− 1(x+ 4)+ 4(y− 3) = 0 − x+ 4y− 16 = 0.

Pozostało znaleźć punkt wspólny prostych 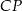i 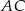(od razu podstawiamy za z drugiego do pierwszego równania)

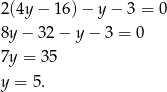
2(4y− 16) − y − 3 = 0 8y− 32− y− 3 = 0 7y = 35 y = 5.

Stąd x = 4 .
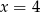Odpowiedź: C = (4,5)

Rozwiązanie Losuj ponownie