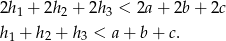Uzasadnij, że suma długości wysokości w dowolnym trójkącie jest mniejsza od jego obwodu.
Oznaczmy boki trójkąta leżące naprzeciwko wierzchołków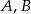 
i 
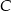przez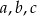 
, a wysokości wychodzące z tych wierzchołków przez 
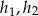i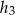 
odpowiednio.
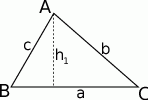
Wysokość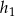 
jest najkrótszym odcinkiem łączącym wierzchołek 
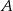z prostą 
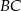, zatem 
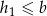i 
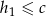. Dodając te nierówności stronami mamy
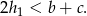
Nierówność jest ostra, bo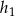 
nie może być jednocześnie równe 
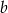i 
. Analogicznie uzasadniamy nierówności
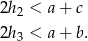
Dodając te trzy nierówności stronami, mamy
Informacje
Zadania
Losowe zadanie
