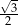Zadanie nr 3416887
W sześcianie o krawędzi długości 2 połączono ze sobą środki trzech ścian mających wspólny wierzchołek. Sporządź odpowiedni rysunek i oblicz pole otrzymanego trójkąta.
Rozwiązanie
Zaczynamy od rysunku.
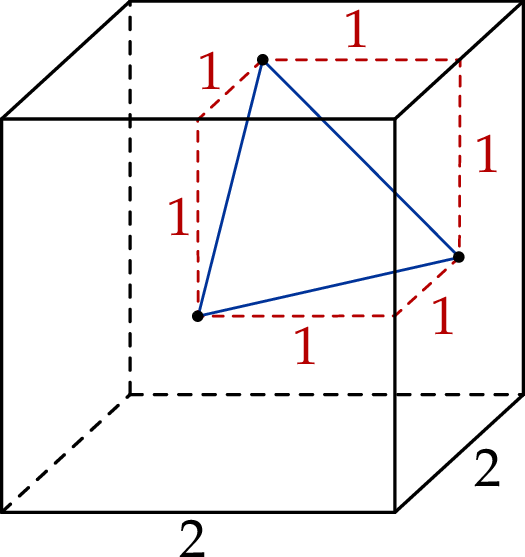
Trójkąt, o którym mowa jest trójkątem równobocznym. Jego bok możemy wyliczyć z twierdzenia Pitagorasa.
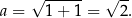
Zatem szukane pole jest równe
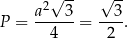
Odpowiedź: